Aufgabe:
Text erkannt:
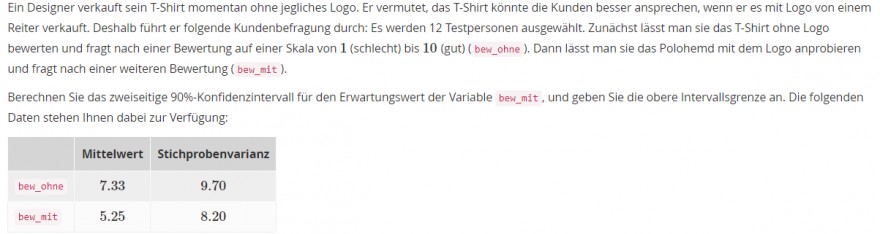
Ein Designer verkauft sein T-Shirt momentan ohne jegliches Logo. Er vermutet, das T-Shirt könnte die Kunden besser ansprechen, wenn er es mit Logo von einem Reiter verkauft. Deshalb führt er folgende Kundenbefragung durch: Es werden 12 Testpersonen ausgewählt. Zunächst lässt man sie das T-Shirt ohne Logo bewerten und fragt nach einer Bewertung auf einer Skala von 1 (schlecht) bis 10 (gut) ( bew_ohne ). Dann lässt man sie das Polohemd mit dem Logo anprobieren und fragt nach einer weiteren Bewertung ( bew_mit).
Berechnen Sie das zweiseitige 90\%-Konfidenzintervall für den Erwartungswert der Variable bew_mit, und geben Sie die obere Intervallsgrenze an. Die folgenden Daten stehen Ihnen dabei zur Verfügung:
\begin{tabular}{lcc}
& Mittelwert & Stichprobenvarianz \\
\hline bew_ohne & \( 7.33 \) & \( 9.70 \) \\
bew_mit & \( 5.25 \) & \( 8.20 \) \\
\hline
\end{tabular}
Problem/Ansatz:
… Mein Rechenweg: 5,25 + 1,6449 * √(8,20/12) = 6,6097
Kann mir jemand ein Hinweis geben wo mein Fehler liegt? LG & Danke