Berechnen Sie das zweiseitige 90%-Konfidenzintervall für den Erwartungswert bew_ohne, und geben Sie die …

Question

Aufgabe:

Ein Designer verkauft sein Hemd momentan ohne jegliches Logo. Er vermutet, das Hemd könnte die Kunden besser ansprechen, wenn er es mit Logo von einem Reiter verkauft. Deshalb führt er folgende Kundenbefragung durch: Es werden 11 Testpersonen ausgewählt. Zunächst lässt man sie das Hemd ohne Logo bewerten und fragt nach einer Bewertung auf einer Skala von 1(schlecht)  bis 10 (gut). (bew_ohne). Weitere 11 Kunden lässt man das Polohemd mit dem Logo anprobieren und fragt nach ihrer Bewertung (bew_mit). Berechnen Sie das zweiseitige 90%-Konfidenzintervall für den Erwartungswert der Variable bew_ohne, und geben Sie die obere Intervallsgrenze an. Die folgenden Daten stehen Ihnen dabei zur Verfügung:

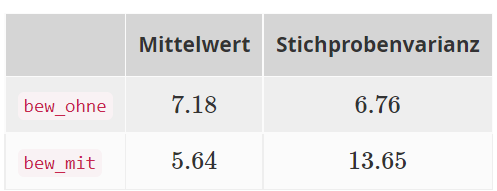
Problem/Ansatz:

Ich komm ständig auf das falsche Ergebnis..

Mein Rechenweg: (1-0.90)/2=0.05 + 0.90= 0.95 -> bei Tabelle ablesen

 -> 1.6449

7.18+1.6449 * Wurzel aus 6.76/11 =  8.4694..~ 8.47

Leider nicht richtig ... bitte um Hilfe

Comments

(1-0.90)/2=0.05 + 0.90

Rechne aus was links vom Gleichheitszeichen steht.

Rechne aus was rechts vom Gleichheitszeichen steht.

Beurteile, ob das Gleichheitszeichen gerechtfertigt ist.

---

Das müsste schon so passen ich habs nur blöd hingeschrieben also:

(1-0.90)= 0.1

0.1/2=0.05

-> 0.05+0.90= 0.95 -> bei Tab. ablesen 1.6449 genau so wie ich es gemacht habe stimmt aber nicht :-S komm nicht auf meinen fehler...

Answer 1

Falls man eine Normalverteilung annehmen soll ist $$ 7.18 + 1.645 \cdot \frac{6.76}{\sqrt{11}} $$ richtig und nicht $$ 7.18 + 1.645 \cdot \sqrt{\frac{6.76}{11}} $$

Comments

Ich würde auch sagen,, dass man hier die T-Verteilung nehmen muss, da die Standarabweichung ja empirisch ermittelt wurde und a-priori bekannt ist.

---

Ah, sorry. Wenn es die Varianz ist, ist es richtig. Ich hatte das überlesen und gedacht das ist die Streuung. Vielleicht hilft die t-Verteilung.