Whe hoch ist die zu erwartende Zusatzpension, wenn eine Verzinsung von 2 Prozent angenommen wird?

Question

Text erkannt:

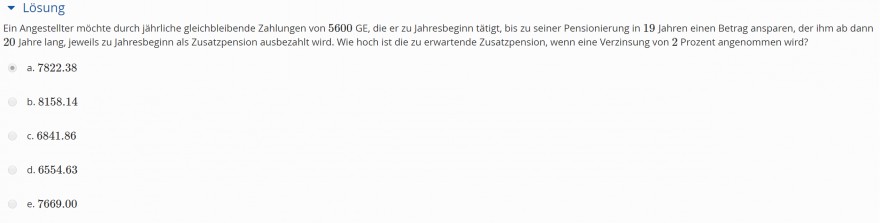
- Lösung Ein Angestellter móchte durch jährliche gleichblelbende Zahlungen von \( 5600 \mathrm{GE} \), die er zu jahresbeginn tatigt, bis zu seiner Pensionierung in 19 jahren einen Betrag ansparen, der ihm ab dann
20 Jahre lang, jeweils zu jahresbeginn als Zusatzpension ausberahlt wird. Whe hoch ist die zu erwartende Zusatzpension, wenn eine Verzinsung von 2 Prozent angenommen wird?
- a. 7822.38
b. 8158.14
c. 6841.86
d. 6554.63
e. 7669.00

 

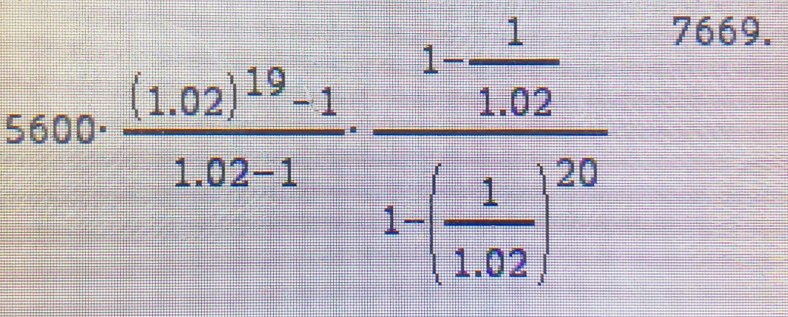
Text erkannt:

\( 5600 \cdot \frac{(1.02)^{19}-1}{1.02-1} \cdot \frac{1-\frac{1}{1.02}}{1-\left(\frac{1}{1.02}\right)^{20}} \)

Wo liegt der Fehler?

Answer 1

5600*1,02*(1,02^19-1)/0,02 = x*1,02*(1,02^20-1)/(0,02*1,02^20)

x=7822,38

Comments

Auf den Wert bin ich auch gekommen, die Lösung ist aber Antwortmöglichkeit a) 7822,38

---

Sorry.

Du muss nach 5600 noch *1,02 ergänzen (vorschüssig).

Habs gerade ediert. :)

---

Mega, hast mir sehr geholfen, Danke !!