Wie löst man folgende Gleichung nach x?

Question

Aufgabe:

Wie löst man folgende Gleichung nach x?

$$ x^{2}+\left(\dfrac{x \cdot b}{x-a}\right)^{2}=h^{2} $$

Comments

Für sowas konsultiere ich halt vielleicht mal Wolfram Alpha.

https://www.wolframalpha.com/input/?i=x%5E2+%2B+%28x*b%2F%28x-a%29%29%5E2+%3D+h%5E2

Hübsche Ergebnisse, nicht wahr ?

---

Hübsche Ergebnisse, nicht wahr ?

Ja, ich bekomme gegen Ende der Seite

Standard computation time exceeded...

---

Das Stichwort "Leiter-Kiste-Aufgaben" hat mir geholfen, herauszufinden, was wohl die dahinter steckende geometrische Aufgabe ist. Ich versuche, sie für weitere Interessierte mal kurz zu beschreiben:

"Durch den Punkt P(a|b) im ersten Quadranten eines x-y-Koordinatensystems verläuft eine fallende Gerade g, welche die x-Achse in X(x|0) mit x>a und die y-Achse in Y(0|y) mit y>b schneidet. Die Länge der Strecke XY sei gleich h. Bestimme die möglichen Werte für x, wenn a,b und h vorgegeben sind." 

Geometrische Situation etwas anschaulicher formuliert:

"Eine Leiter der Länge h ist auf horizontalem Grund stehend schräg an eine senkrechte Wand gestellt. Dabei berührt sie gerade die Oberkante einer quaderförmigen Kiste der Breite a und Höhe b, welche genau in die Ecke zwischen Boden, Wand und Leiter passt." 

So gesehen also eine relativ einfache und durchaus interessante geometrische Frage !

Answer 1

\(\begin{aligned} x^{2}+\left(\dfrac{x\cdot b}{x-a}\right)^{2} & =h^{2} &  & \text{Potenzgesetze}\\ x^{2}+\dfrac{\left(x\cdot b\right)^{2}}{\left(x-a\right)^{2}} & =h^{2} &  & |\cdot\left(x-a\right)^{2}\\ x^{2}\left(x-a\right)^{2}+\left(x\cdot b\right)^{2} & =h^{2}\left(x-a\right)^{2} &  & \end{aligned}\)

Comments

In der dritten Zeile stimmt die rechte Seite nicht.

---

Ich komme da nach dem zweiten Umformungsschritt (bei der Multiplikation mit  (x-a)² )  auf was anderes ...

Answer 2

Wenn du hier eine Lösung in allgemeiner Form anstrebst, wird das eher etwas ungemütlich. Deshalb meine Rückfrage:  Soll das wirklich in aller Allgemeinheit gelöst werden?

Das Ganze führt natürlich auf eine Gleichung 4. Grades - und die allgemeine Lösung dafür ist, sagen wir mal, meistens komplex ...

Comments

Zunächst Danke für die Antwort.

Ja, das soll bitte in aller Allgemeinheit gelöst werden.

Bin kein Mathematiker und desshalb mehr als erstaunt, dass ich beim Versuch, ein geometrisches Problem zu lösen, auf eine Gleichung gestossen bin, bei deren allgemeiner Lösung sogar Wolfram ALpha "den Geist aufgibt".

Etwas meine ich schon herausgefunden zu haben:

Die Gleichung hat abhängig von a, b und h entweder keine, eine oder zwei Lösung(en).

---

Dass Wolfram Alpha "den Geist aufgibt", stimmt doch gar nicht ! Bei mir erscheinen da sämtliche Lösungen, allerdings in Form ellenlanger Terme.

Dass dabei gar nichts echt Komplexes auftritt (i kommt nirgends vor), hat mich erstaunt.

---

Jetzt versteh ich gar nichts mehr. Vor zwei Tagen sah Wolfram Alpha noch ander aus und brachte auch andere Ergebnisse. Gibt es von Wolfram Alpha verschiedene Versionen?

Anyway.

Ich kann das Ergebnis nicht richtig interpretieren. Nicht weil es so ellenlang ist, sondern weil mehrere Lösungen kommen, die aber nach erster Sichtung gleich aussehen.

Auch gibt es definitiv, abhängig von a,b und h, entweder zwei, eine oder keine Lösung(en). Müsste da nicht irgendwo eine Diskriminante sein?

---

Es hat schon seinen Grund, warum Leiter-Kiste-Aufgaben immer mit würfelförmigen Kisten formuliert werden.

---

Naja, von Wolfram α  gibt es schon unterschiedliche Versionen. Für die Profi-Variante bezahlt man auch etwas. Es kann (bei der unbezahlten Version) vorkommen, dass man bei allfällig nur leicht unterschiedlicher Eingabe trotzdem an Grenzen der Gratisversion stößt (Meldung: Standard computation time exceeded...)

Bei den einzelnen angegebenen Lösungen sind ja schon jeweils (Diskriminanten-) Bedingungen angegeben, welche vorausgesetzt werden müssen. Dies sind jeweils ellenlange Ungleichungen.

---

...Leiter-Kiste-Aufgaben...

Daran wurde ich auch erinnert. :-)

Answer 3

1. Formel in die polynomtypische Form bringen:

Substitution 1: h²=c
x^2 + (x*b/(x-a))^2=c
(b^2 x^2)/(a^2 - 2 a x + x^2) + x^2=c |*(a^2 - 2 a x + x^2)
(b^2 x^2)+x²*(a^2 - 2 a x + x^2)=c*(a^2 - 2 a x + x^2)
-a^2 c + a^2 x^2 + 2 a c x - 2 a x^3 + b^2 x^2 - c x^2 + x^4=0
x^4 +(- 2 a)*x³ +(a^2+ b^2-c)*x² + (2 a c)*x -a^2*c =0 Polynom Grad 4 -> lösbar mit der universellen PQRSTUVW-Formel (kein Schulstoff! -> Lehrer nutzen nur Spezialfälle, wo sich Teile herauskürzen oder Nullstellen leicht zu erraten sind!)

https://upload.wikimedia.org/wikipedia/commons/9/99/Quartic_Formula.svg

Der universelle Polynom-Nullstellenrechner unter

https://www.lamprechts.de/gerd/php/gleichung-6-grades.php

nutzt die alte Cardanische Formel (noch mit Fallunterscheidung) und die neue PQRSTUVW-Formel (analog zur PQRST-Formel für Gleichungen 3. Grades

https://www.lamprechts.de/gerd/Bilder/QuadratischeGleichung_p-q-Formel_KubischeGleichung_PQRST-Formel.png )

Substitution 2 für die 4 Faktoren:
k3=- 2 a
k2=a^2+ b^2-h²
k1=2*a*h²
k0=-a²*h²

Probe:
a=1/2=0.5
b=3
h=4
Subst:
k3=-1
k2=(1/2)^2+ 3^2-4² = -6.75
k1=1*4²=16
k0=-(1/2)²*4²=-4

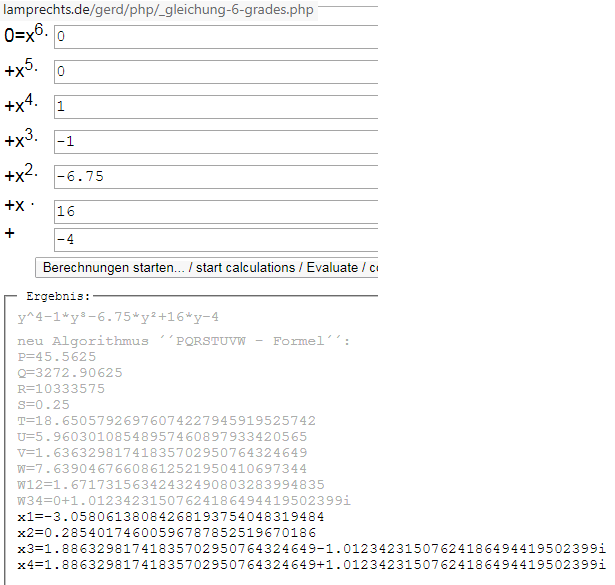
############### neu Algorithmus ´´PQRSTUVW - Formel´´: #############

P=45.5625
Q=3272.90625
R=10333575
S=0.25
T=18.65057926976074227945919525742
U=5.96030108548957460897933420565
V=1.63632981741835702950764324649
W=7.63904676608612521950410697344
W12=1.67173156342432490803283994835
W34=0+1.01234231507624186494419502399 i  {komplexes Zwischenergebnis ! }

Polynome vom Grad 4 haben immer 4 Lösungen! Hier sind 2 komplex:
x1=-3.05806138084268193754048319484
x2=0.28540174600596787852519670186
x3=1.88632981741835702950764324649-1.01234231507624186494419502399i
x4=1.88632981741835702950764324649+1.01234231507624186494419502399i
Probe für die beiden reellen Lösungen:

x^2+(x*3/(x-1/2))^2,x=-3.05806138084268193754048319484

ergibt 16
x^2+(x*3/(x-1/2))^2,x=0.28540174600596787852519670186

ergibt 16

Hinweise:

Bei dieser langen PQRSTUVW-Formel muss man Fehlerfortpflanzung beachten!

Wer also mit einem Billig-Taschenrechner nur 4 Nachkommastellen verwendet, wird vermutlich nur 1 Nachkommastelle richtig haben -> da ist man mit Newton-Näherungsverfahren schneller & genauer

und bracht für die reellen Nullstellen keine komplexen Zwischenergebnisse.

Die komplexen Zwischenergebnisse entstehen überall dort, wo Argumente von Wurzeln negativ sind:

- sqrt(x)=x^(1/2)= 2. Wurzel von x

- x^(1/3)= 3. Wurzel von x

Wenn man nicht genau genug rechnet, können auch komplexe Reste überbleiben, die in Wirklichkeit nicht vorhanden sind.

Vorteil dieser universellen Formel: die k-Faktoren  selbst können auch komplex sein ( das ist mit Newton-Verfahren dann nur sehr umständlich lösbar)

Für "Leiter-Kiste" Sonderfall reichen meist Näherungen oder die Umwandlung mit trigonometrischen Formeln  (siehe http://www.mathematische-basteleien.de/leiter.htm ), was dem Spezialfall:

Cardanische Formeln 1 von 3 Fällen entspricht).