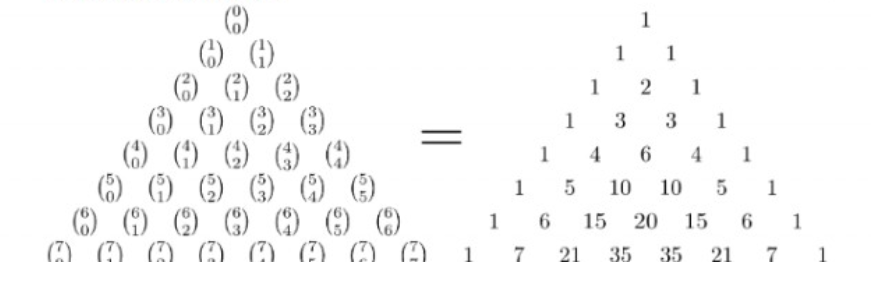Aufgabe:
Beweisen Sie durch Anwenden und Umformen der Definition
$$ \left(\begin{array}{l} n \\ k \end{array}\right)=\frac{n !}{k !(n-k) !} \text { für } n, k \in \mathbb{N} \text { und } k \leq n $$
die folgenden Eigenschaften des Binomialkoeffizienten:
a) \( \left(\begin{array}{c}n \\ n-k\end{array}\right)=\left(\begin{array}{c}n \\ k\end{array}\right) \) (Symmetrie)
b) \( \left(\begin{array}{l}n \\ 1\end{array}\right)=\left(\begin{array}{l}n \\ n-1\end{array}\right)=n, \) falls \( n \geq 1 \) (Randwerte)
c) \( \left(\begin{array}{c}n+1 \\ k\end{array}\right)=\left(\begin{array}{c}n \\ k-1\end{array}\right)+\left(\begin{array}{c}n \\ k\end{array}\right) \) für \( 1 \leq k \leq n \) (Rekursionsformel)
und veranschaulichen Sie jede dieser Eigenschaften im Pascal'schen Dreieck, dessen Einträge natürliche Zahlen sind.
Unten sehen Sie zwei Darstellungen des Pascal'schen Dreiecks links mit Binomialkoeffixienten, rechts mit arabischen Ziffern.