Die Koch'sche Schneeocke ist gegeben durch folgende Konstruktion:
Frau Holle hat ihr Rexept für Schneeflocken verloren. Helfen Sie ihr! Die Koch'sche Schneeflocke ist gegeben durch folgende Konstruktion:
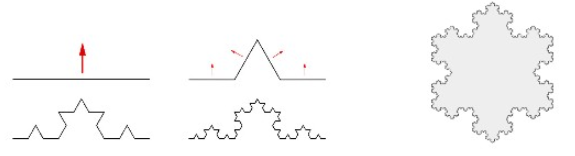
Gegeben sei ein gleichseitiges Dreieck. Im ersten Schritt teilt man jede in drei gleich lange Streckenstücke und setzt auf das mittlere Streckenstück ein gleichsseitiges Dreieck, dessen Seiten jeweils so lang sind wie jeweils die drei Teilstrecken der Ausgangsseite. Im zweiten Schritt wiederholt man dies auf jedem neu entstandenen Streckenstück, vgl. Abbildungen. Der Grenzwert der entstehenden Figurenfolge wird als Koch'sche Schneeflocke bezeichnet.
a) Zeigen Sie: Die Koch'sche Schneeflocke besitzt keinen endlichen Umfang.
b) Zeigen Sie: Die Koch'sche Schneeflocke besitzt einen endlichen Flächeninhalt. Berechnen Sie diesen.
c) Malen Sie ein Weihnachtsbild, in dem eine Iteration (mindestens nach dem zweiten Schritt oder höher) der Koch'schen Schneeflocke auftaucht. Hierbei sind Ihrer Kreativität keine Grenzen gesetzt.
Die drei kreativsten Lösungen (unter der Bedingung, dass (a) und (b) auch bearbeitet wurden) werden in den jeweils letzten Vorlesungen vor Weihnachten am 19. bzw. 20. Dezember mit hausgemachtem Gebäck prämiert.