Hallo Ich habe folgende Aufgabe:
Der Weihnachtsmarkt ist unter Studenten ein beliebter Treffpunkt um sich von den Strapazen des anstrengenden Universitätsalltages zu erholen. Hierbei verspüren zwei von fünf Studenten ein starkes Hungergefühl, sobald sie den Weihnachtsmarkt betreten haben. Die Currywurst, ein Klassiker am Weihnachtsmarkt, wird von 80 Prozent der hungrigen (!) Studenten als Speise bevorzugt. Die anderen hungrigen Studenten essen gerne Flammkuchen. Durstig sind alle Studenten. Gegessen wird jedoch als erstes. Diejenigen, die keinen Hunger hatten, entscheiden sich zu 90% für den Genuss eines Glühweins. Nur 10% von ihnen probieren die Odenwälder Feuerzangenbowle. Auf Grund der unmittelbaren Nachbarschaft des Flammkuchen- und des Feuerzangenbowlenstandes, entscheidet sich je- doch jeder zweite Student, der einen Flammkuchen gegessen hat, für die Feuerzangenbowle. Die restlichen Flammkuchenverzehrer trinken Glühwein am Feuerzangenbowlenstand. Unter den Freunden der gepflegten Currywurst sieht die Sache ganz anders aus. Denen ist der Feuerzangenbowlenstand zu weit weg, so dass 70 % zum gegenüberliegenden Glühweinstand wechseln. Der hohe Schärfegrad der Currywurst animiert die restlichen 30% zum Verzehr einer Cola direkt am Imbiss. Zur Vereinfachung der Aufgabe nehmen wir abschließend an, dass jeder Student genau ein Getränk und höchstens eine Speise konsumiert.
Das Ergibt folgenden Wahrscheinlichkeitsbaum.
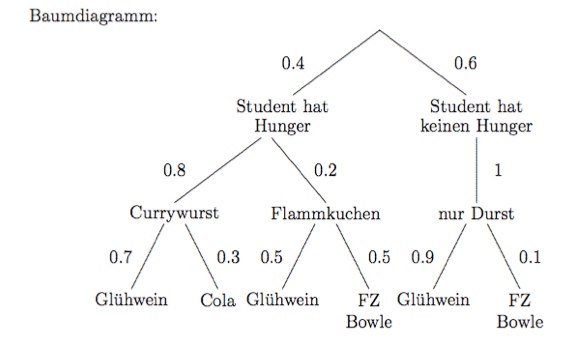
Hinzu kommt Pierre:
Pierre mag keine Currywurst. Sollte er beim Betreten des Weihnachtsmarktes Hunger bekommen, so wird er sich auf jeden Fall einen Flammkuchen kaufen.
Dem Weihnachtsmarkt ging in der letzten Woche die Cola aus. Sämtliche Studenten die eine Currywurst genossen haben mussten anschließend Ihren Durst mit Glühwein stillen. Hat dies einen Einfluss auf die (Un)abhängigkeit des Ereignispaares ’Student trinkt Glühwein’ und ’Student hat Hunger’:
Dazu habe ich:
p(Glühw | ! Hungrig) = 0.9
p(FZB | ! Hungrig) = 0.1
p(Cola | ! Hungrig) = 0
p(Glühw | Hungrig) = 0.1 + 0.56 = 0.66
p(Cola | Hungrig) = 0.24
p(FZB | Hungrig) = 0.1
Wie liegen die Abhängigkeiten im Fall von Pierre?
Dazu heißt es in der Lösung:
Sollte Pierre keinen Hunger haben, so stehen die Chancen Glühwein zu Feuerzangenbowle bei \(90\) zu \( 10 . \) Hat er jedoch Hunger, so steht es \(50\) zu \( 50 . \) Die Abhängigkeit ist also eindeutig. Formal:
$$ \begin{array}{c} {P(\text { FZBowle (Pierre) } \cap \text { Hunger (Pierre) })=0.4 \cdot 1 \cdot 0.5=0.2, \text { während }} \\ {P(\text { FZBowle (Pierre) }) \cdot P(\text { Hunger (Pierre) })=(0.4 \cdot 1 \cdot 0.5+0.6 \cdot 1 \cdot 0.1) \cdot 0.4} \end{array} $$
\( =0.104 \)
Mir erschließt sich nun NICHT was die zweite Aussage bedeutet.
Die Erste ist ja die Wahrscheinlichkeit, dass Pierre FZB Trinkt und dass er auch noch Hungrig ist.
vgl.(c) 2008
Fachbereich Mathematik - TuDarmstadt
Prof. Dr. W. Stannat & A. Janoschek