Höhenlinien der Funktion z=f(x ; y)=3 x - 5 y?

Question

Aufgabe: Darstellung von Funktionen:

 Skizzieren Sie die Höhenlinien der folgenden Funktionen.

3) \( z=f(x ; y)=3 x-5 y \)
4) \( z=f(x ; y)=\sqrt{y-x^{2}} \quad \) Beachten Sie den Bereich, in dem die Funktion definiert ist.

Answer 1

Hallo,

pick dir verschiedene Werte raus, z. B. \(f(x,y)=3x-5y=0\), dann hast du \(y=\frac{3}{5}x\). Wenn du das für viele Werte machst, erhältst du folgendes Bild:

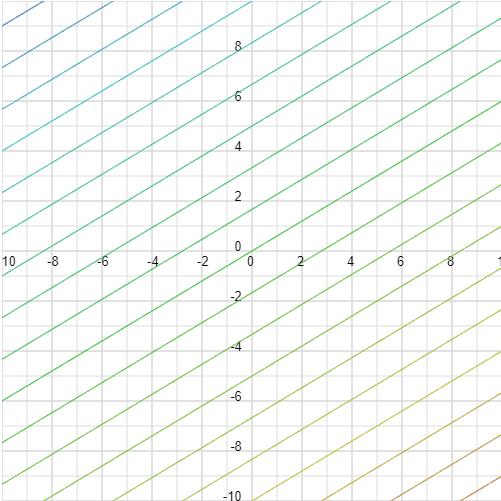
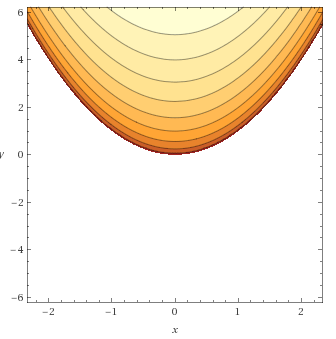
Für \(z=f(x ; y)=\sqrt{y-x^{2}} \) analog, obwohl \(y\geq x^2\) sein muss, also nicht beliebige Werte genommen werden können. Hier nehme ich auch \(f(x,y)=0\), dann hast du \(y=x^2\). Für \(f(x,y)=1\) hast du \(y=x^2+1\). Also die Normalparabel immer um den Wert der Höhenlinie nach oben verschoben.

 

Comments

Ich hab das jetzt so aufgeschrieben, aber ganz verstanden habe ich es noch nicht, danke dir trotzdem

---

Guck dir mal vielleicht dieses Video an: