Beweis des Ähnlichkeitssatzes WW (mithilfe des Kongruenzsatzes WSE; ohne zentrische Streckung und ohne Strahlensatz)
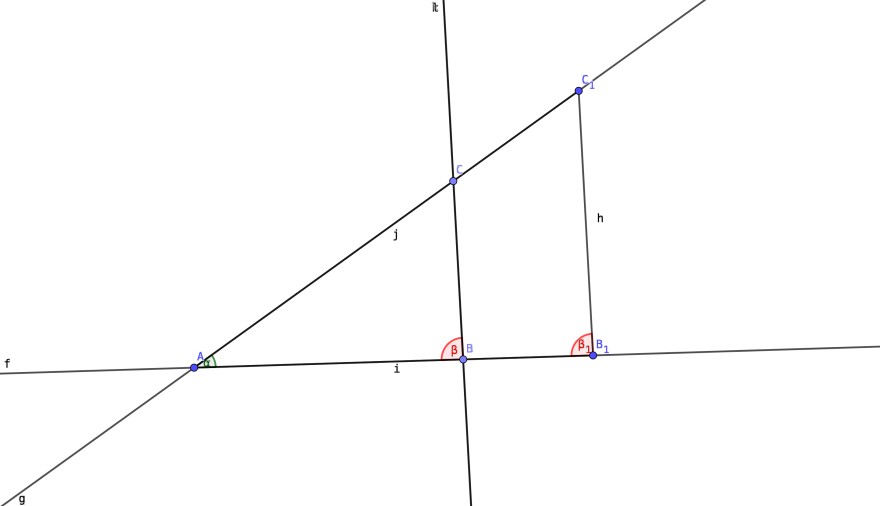
Gegeben sind die Dreiecke ABC und A1B1C1.
Es gilt, dass α=α1 und β=β1 und damit natürlich auch γ=γ1.
Da B und B1 beide auf dem selben Strahl liegen, gibt es ein k, mit c1=k*c. Wenn man also Strecke c des Dreiecks ABC so verlängert, dass gilt c=c1 und dabei die beiden Winkel α und β invariant lässt, erhält man mit Kongruenzsatz WSW ein Dreieck welches kongruent ist zu A1B1C1. Somit ist das entstandene Dreieck ähnlich zu A1B1C1.
Jetzt komme ich nicht weiter:
Klar ist, dass c1=k*c gilt (nach Konstruktion).
Ferner gilt a1=k' *a und b1=k'' * b.
Wie kann ich zeigen (ohne die oben ausgeschlossenen Hilfsmittel), dass k=k'=k'' ?
Vielen Dank :)!