1. Gegeben sind die Gerade gAC: y=1/2x+3,5 und die Punkte A(-2 | 2,5); B(3 | -5) und C(c1 | c2).
Die Koordinaten des Punktes C= gAC(bogen)gBC sollen so gewählt sein, dass gAC senkrecht zu gBC ist.
a) Berechnen Die Gleichungen der Geraden gAB, gBC und ihren Scnittpunkt C!
C[x, 1/2x + 3.5]
m(BC) = (1/2x + 3.5 + 5) / (x - 3) = -1/(1/2)
x = -1
C[-1, 1/2*(-1) + 3.5] = C[-1, 3]
b) Zeichnen Sie die drei Gleichungenin ein KKS und berechnen Sie den Abstand hC des Punktes C von gAB!
Abstand von C nach B
|CB| = √((3 + 5)^2 + (-1 - 3)^2) = 4·√5
Skizze:
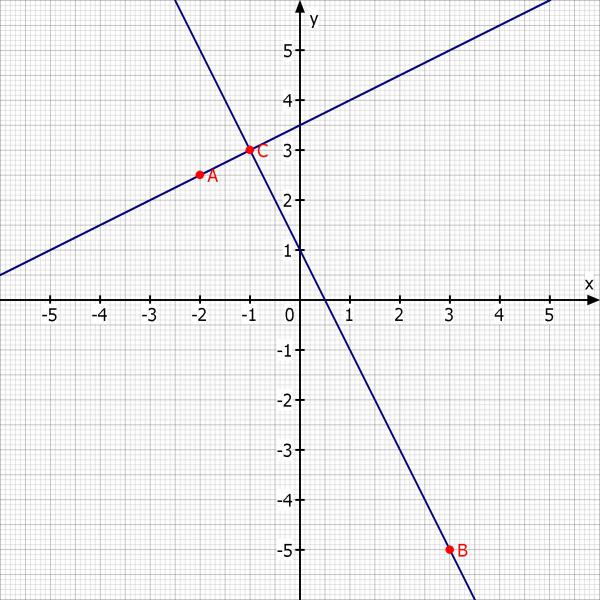
c) Geben Sie die kleinste Produktmenge J1xJ2 aus den zwei Intervallen J1 und J2 in der das DreieckABC liegt, und bestimmen Sie den F1 A des Dreiecks und seine Winkel alpha, beta und gamma.
|AC| = √5/2
A = 1/2 · √5/2 · 4·√5 = 5
Gamma ist 90 Grad.
Alpha = arctan(4·√5 / (√5/2)) = 82.87 Grad
Beta = 180 - 82.87 = 97.13 Grad
Das mit den Intervallen ist mir aber unklar. Ist dort das x Intervall und das y-Intervall gemeint?