Noch zwei mal Quadratische Funktionen

Question

erstmal vielen, vielen Dank für die Mühe beim beantworten meiner letzen Frage!

hier sind meine 2 letzten Problemfälle.

Aufgabe1: Gegeben ist die Funktion f durch ihre Gleichung : y=f(x)=x²-2sx-1
a) Ermitteln sie die Koordinaten des Scheitelpunktes und zeichnen sie den Graph dieser Funktion mindestens im Intervall 3<x<3 in ein Koordinatensystem.

b) Prüfen sie rechnerisch ib x=2,5 eine Nullstelle der Funktion f ist.

c) Zeichnen Sie in dasselbe Koordinatensystem eine Gerade g, die den Graph der Funktion f in genau zwei Punkten schneidet und nicht parallel zur x-Achse verläuft. Die Gerade g ist das Bild einer lineareFunktion.
Geben sie deren Funktionsgleichung an.

 

Aufgabe 2:

a) Durch die Gleichung y=f(x)=(x-1,8)²-4 (x ∈ R) ist eine Funktion gegeben. Zeichnen sie den Graph dieser Funktion mindestens im Intervall -1<x<4! Und berechnen sie die Nullstellen der Funktion

b)Welche Zahl ist in die Gleichung y=(x)=x²-3,6x+q

für q einzusetzen damit die dadurch gegebene Funktion genau eine Nullstelle hat?

 

Ich danke schonmal für im Voraus - echt super Arbeit die hier gemacht wird!

Answer 1

Bei Aufgabe 1 ist ein Parameter s enthalten. So kann man die Funktion nicht zeichnen. Es sollte dann ein Wert für s angegeben sein für den man es zeichnen soll. Ebenso die Nullstellen. Das wäre so nur in Abhängigkeit von s zu lösen.

 

Aufgabe 2:

a) Durch die Gleichung y = f(x) = (x - 1,8)² - 4 (x ∈ R) ist eine Funktion gegeben. Zeichnen sie den Graph dieser Funktion mindestens im Intervall -1<x<4! Und berechnen sie die Nullstellen der Funktion

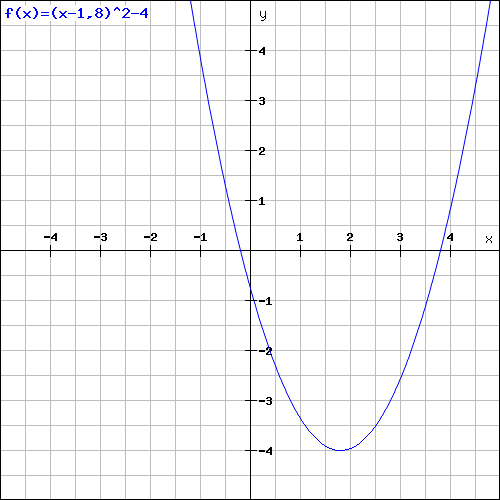
f(x) = 0 

(x - 1,8)² - 4 = 0

 

(x - 1,8)²  = 4

x - 1,8  = +-2

x - 1,8  = +-2

x1 = 2 - 1,8 = 0,2

x2 = -2 - 1,8 = -3,8

b)Welche Zahl ist in die Gleichung y=(x)=x² - 3,6x + q für q einzusetzen damit die dadurch gegebene Funktion genau eine Nullstelle hat?

Scheitelpunkt ist bei 

x = -p/2 = +3,6/2 = 1,8

Das setzen wir also für x ein um die y-Koordinate zu berechnen

f(1,8) = (1,8)² - 3,6*(1,8) + q = - 81/25 + q

q sollte daher 82/25 sein. Damit der Scheitelpunkt auf der x-Achse liegt.

Ich danke schonmal für im Voraus - echt super Arbeit die hier gemacht wird!