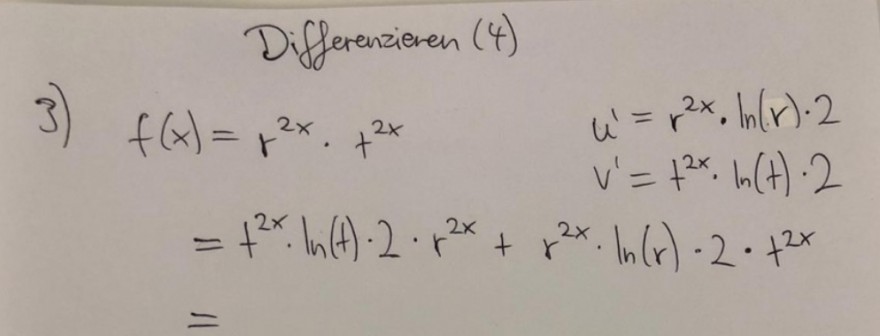Moin Freunde!
Kann mir jemand erklären, wie ich von meinem Stand auf die Lösung komme?
Ich weiß nämlich nicht wie man das so zusamenfassen kann..
Vielen Dank für Antworten!
Aufgabe:
\( f(x)=r^{2 x} * t^{2 x} \)
\(\rightarrow f^{\prime}(x)=2 \ln (r t)(r t)^{2 x} \)