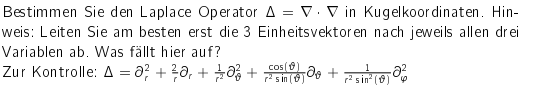
Text erkannt:
Bestimmen Sie den Laplace Operator \( \Delta=\nabla \cdot \nabla \) in Kugelkoor dinaten. Hinweis: Leiten Sie am besten erst die 3 Einheitsvektoren nach jeweils allen drei Variablen ab. Was fallt hier auf?
$$ \text { Zur Kontrolle: } \Delta=\partial_{r}^{2}+\frac{2}{r} \partial_{r}+\frac{1}{r^{2}} \partial_{\theta}^{2}+\frac{\cos (\theta)}{r^{2} \sin (\theta)} \partial_{\theta}+\frac{1}{r^{2} \sin ^{2}(\theta)} \partial_{\varphi}^{2} $$
Wie kann ich den Einheitsvektor nach allen drei Variablen ableiten, fällt dann nicht einfach nur jeweils die x, y bzw. z Komponente weg?
Und wenn ja, dann hat sich mein Ergebnis irgendwie komisch doppelt gemoppelt so dass sich die r rauskürzen.
Über einen Ansatz oder Hinweise auf meinen Denkfehler würde ich mich sehr freuen.