ich brauche dringend Hilfe bei diesen Aufgaben.
a)Begründe sin(alpha)=cos(alpha)=tan(alpha) das Thema sind perodische Prozesse
b)Eine Grafik und Arbeitsblatt von unserem Lehrer welches wir benutzen dürfen.Die letzten drei Aufgaben kann ich echt nicht nachvollziehen.Wäre nett wenn mir jemand ein Überblick geben würde gerne auch zu den Vorherigen zum Verständnis.
Danke danke danke :)))
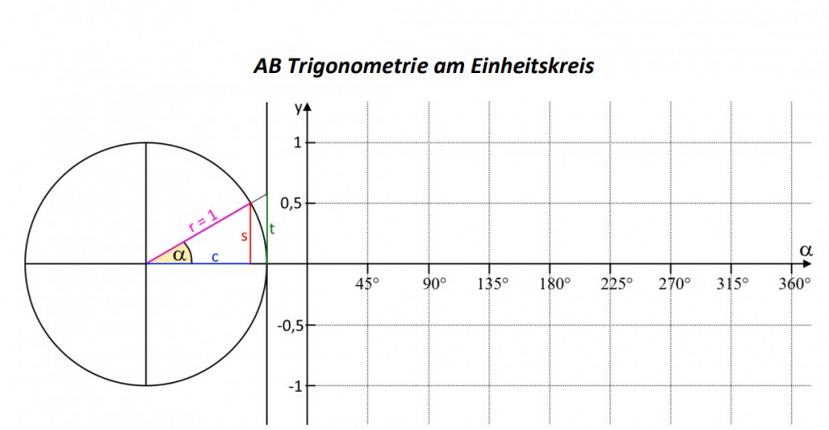
Ein Einheitskreis ist ein Kreis mit Radius \( r=1 \) (Längeneinheit \( = \) LE ). Alle Angaben sind dann Vielfache von LE.
a) Das \( A B \) ist nicht bunt ausgedruckt? Zeichne die Strecken jeweils in einer Farbe nach (z.B. rot, blau, grün).
b) Begründe, dass Folgendes gilt: \( s=\sin (\alpha), c=\cos (\alpha), t=\tan (\alpha) \)
c) Für den hier gezeichneten Winkel ist \( s=0,5 . \) Miss den Winkel und trag das Wertepaar (Winkel I Sinuswert) in der passenden Farbe in das Koordinatensystem ein.
d) Miss nun s (in LE) für die Winkel \( \alpha=15^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}, 75^{\circ} \) und \( 90^{\circ} \). (Zeichne verschiedene Radien ein.) Prüfe mit dem Taschenrechner, ob du richtig gemessen hast.
Der große Vorteil des Einheitskreises ist: Man kann nun auch den Winkel über \( 90^{\circ} \) hinaus vergrößern und auch hierfür Sinus, Kosinus und Tangens definieren - siehe Bild.
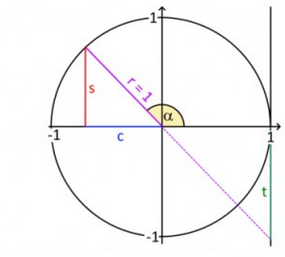
e) Überlege nun mit Hilfe von Symmetrien, welche Werte für \( \sin (\alpha) \) entstehen, wenn \( \alpha=105^{\circ}, 120^{\circ}, 135^{\circ}, \ldots \) ist. Schaffst du es, bis \( \alpha=360^{\circ} \) zu kommen?
Ergänze dann die Messpunkte zu einem Graphen!
Achtung: Der Radius ist \( r=\quad \mathrm{cm}, \) was nun einer Längeneinheit (1 LE) entspricht. Teile daher alle
\( \mathrm{cm}- \) Maße durch _____, um die Längen in \( L E \) anzugeben und ins Koordinatensystem eintragen zu können!
f) Miss nun auch \( c=\cos (\alpha) \) für alle diese Winkel. Trage die Wertepaare und schließlich den Graphen in der passenden Farbe ein.
g) Und nochmal das gleiche Spiel für \( t=\tan (\alpha) . \) Beachte, dass t immer auf der rechten Tangente liegt.
Knobibonus für Experten: Schaffst du es, eine entsprechende Konstruktion mit GeoGebra zu erstellen?