\(f(x)=x^2+4x+3\)
Kurventangente parallel zur Geraden \(g(x)= \green{5}x+10\)?
Die Schnittpunkte der Geraden mit der Parabel findet man, wenn \(f(x)=g(x)\) gesetzt werden.
\(x^2+4x+3= 5x+10\)
\(x^2-x= 7\)
\((x-0,5)^2= 7+0,25=7,25 |±\sqrt{~~}\)
\(x-\red{0,5}=±\sqrt{ 7,25 }\)
Rechne ich jetzt weiter, so erhalte ich die beiden x-Stellen der Schnittpunkte .
Die benötige ich aber nicht, sondern nur den Berührpunkt der Kurventangente parallel zur Geraden \(g(x)= 5x+10\).
Die Berührstelle der Tangente liegt nun bei \(x=\red{0,5}\)
Berührpunktkoordinate \(B(0,5|5,25)\)
Die Tangentensteigung beträgt \(m=\green{5}\)
Die allgemeine Punkt-Steigungsform einer Geraden lautet: \( \frac{y-y_1}{x-x_1}=m \)
Hier :\( \frac{y-5,25}{x-0,5}=5 \)
\(y=5x+2,75\)
Dieses ist nun die gesuchte Tangente an die Parabel.
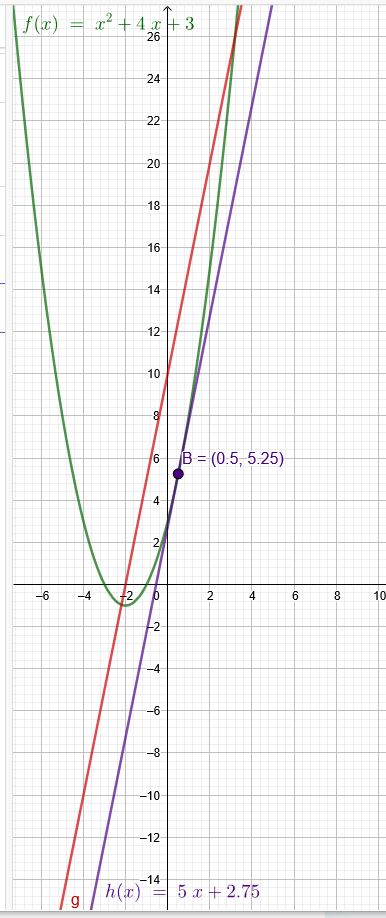
Leider ist dieses Verfahren nur bei quadratischen Parabeln erfolgreich.