Hallo Julia,
(1) Definiere "Stern"! Ich postuliere mal ein Stern entsteht, wenn man eine ungerade Anzahl \(n\) von Punkten auf dem Umfang eines Kreises plaziert und sie mit einem geschlossenen Polygonzug derart verbindet, dass jeweils der \(i\)'te Punkt mit dem \(((i + (n-1)/2) \mod n)\)'ten Punkt verbunden ist. Die Punkte müssen dazu nicht zwingend gleichmäßig verteilt sein.
Beim regelmäßigen Fünfeck kann das so aussehen:
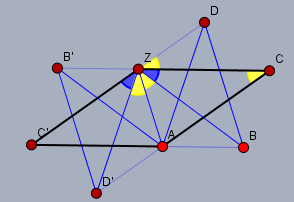
ist aber noch zu speziell - allgemein kann man es wohl besser beim 7-eckigen Stern zeigen:
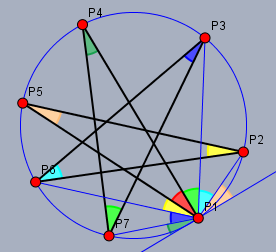
(2) es gibt ja diese bekannten Bilder vom Beweis des Satzes von Pythagoras. Hier ist es ähnlich:
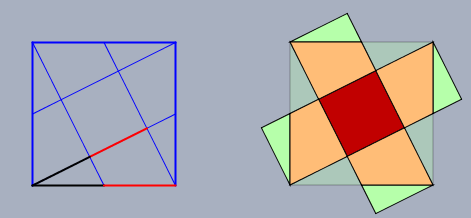
(3) s. Anwort von MontyPython
(4) Wikipedia kennst Du doch. Da findet man dann unter der Fibonacci-Folge auch das passende Bild zu $$\sum_{i=0}^n F_i^2 = F_n \cdot F_{n+1}$$
Falls Du dazu noch Frage hast, so melde Dich bitte.
Gruß Werner