1. Einführung
Beweise in der Mathematik müssen nicht immer kompliziert sein - im Gegenteil. Viele Beweise können anschaulich und ohne komplizierte Formeln jedem zugänglich gemacht werden. Überzeuge dich selbst bei diesem geometrischen Beweis des kleinen Gauß (Gauß'sche Summenformel) ohne vollständige Induktion!
2. Der Beweis
Der kleine Gauß beschreibt den folgenden Zusammenhang:
\(1+2+3+...+n=0,5\cdot n\cdot (n+1)\)
Dabei ist \(n\in\mathbb{N}\) eine natürliche Zahl. Mit Hilfe des Summenzeichens kann diese Formel wie folgt verkürzt notiert werden:
\(\sum\limits_{k=1}^{n}{k}=0,5\cdot n\cdot (n+1)\)
Für eine geometrische Interpretation betrachtest du zunächst einen quadratischen Block mit der Seitenlänge \(1\):
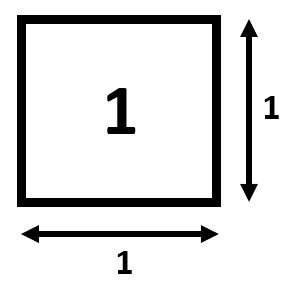
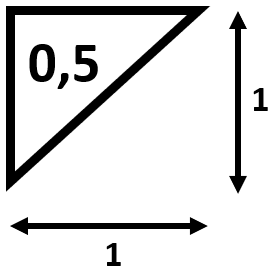
Halbierst du diesen quadratischen Block entlang einer Flächendiagonalen, so erhältst du ein Dreieck mit dem Flächeninhalt \(0,5\).
Der Zusammenhang wird nun vereinfacht dargestellt (d. h. es wird auf Punkte zur Andeutung von allen Summanden zwischen \(3\) und \(n\) verzichtet). Man kann die Summe der ersten \(n\) aufeinanderfolgenden natürlichen Zahlen (unter Berücksichtigung der zuvor erwähnten Vereinfachung) geometrisch wie folgt auffassen:
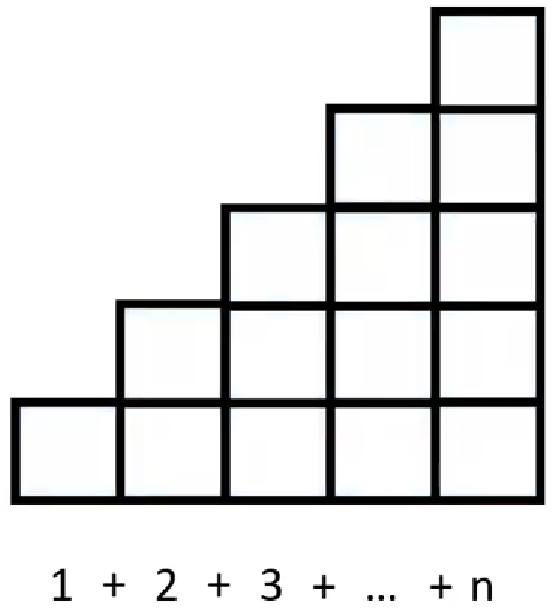
Gesucht ist nun der blau markierte Flächeninhalt:
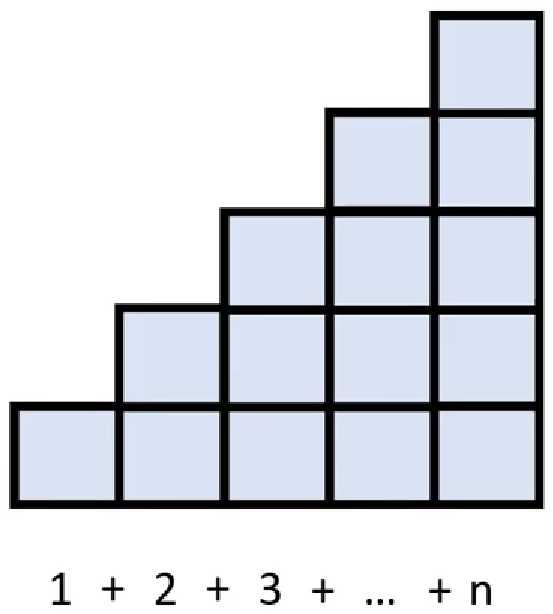
Diesen kannst du errechnen, indem du zuerst das Quadrat mit dem Flächeninhalt \(n\) betrachtest:
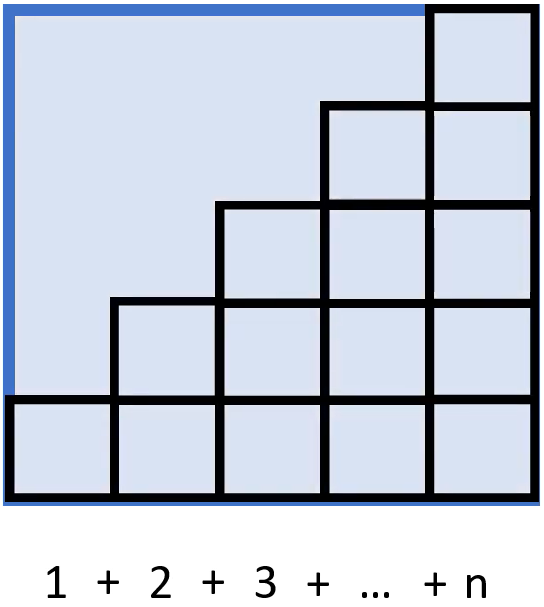
Die blau markierte Fläche hat also einen Flächeninhalt von $$n\cdot n$$ Halbierst du diesen, erhältst du den Flächeninhalt der markierten Dreiecksfläche:
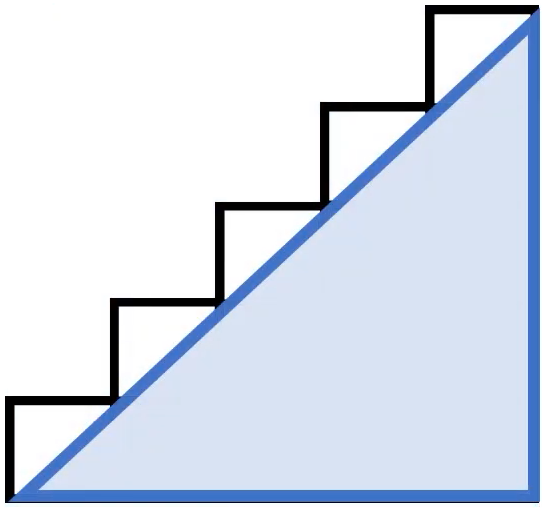
Diese besitzt den Flächeninhalt $$0,5\cdot n\cdot n$$ Das reicht aber offensichtlich noch nicht, denn es soll der Flächeninhalt der gesamten Figur (= Wert der Summanden von \(1\) bis \(n\)) ermittelt werden. Es fehlen noch die insgesamt \(n\) grün markierten Dreiecksflächen, die jeweils einen Flächeninhalt von \(0,5\) besitzen:
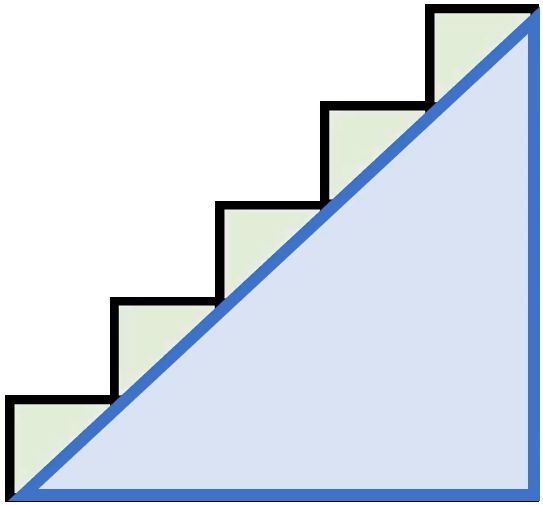
Wenn du diese \(n\) Flächen mit dem Flächeninhalt \(0,5\) auf die Dreiecksfläche mit dem Flächeninhalt \(0,5\cdot n\cdot n\) addierst, erhältst du:
\(0,5\cdot n\cdot n+0,5\cdot n\)
Klammere den Faktor \(0,5\cdot n\) aus und Du erhältst das Ergebnis:
\(0,5\cdot n\cdot (n+1)\)
\(\square\)
In dem eingangs geposteten Video habe ich diese Vorgehensweise animiert. Mich würde euer Feedback sehr freuen :)
André
Dieser Artikel hat 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.
