Dies ist Teil 1. Hier geht es um die theoretischen Grundlagen der Aussagenlogik. Der Fall wird in Teil 2 gelöst.

1. Einführung
Dieser Artikel ist ein Versuch, die von einigen Studenten als „trocken“ empfundene Theorie der Aussagenlogik auf humoristische Art und Weise zu vermitteln. Wir begleiten dabei den Oberschülerdetektiv Shinichi Kudo bei der Lösung eines Falls. Die Schlussfolgerungen basieren dabei auf den Prinzipien der Aussagenlogik.
Hinweis: Die Figuren bzw. das Setting stammen aus dem Anime „Meitantei Konan“ (zu Deutsch: Detektiv Conan, https://de.wikipedia.org/wiki/Detektiv_Conan)
2. Der Fall
Oberschülerdetektiv Shinichi Kudo hilft der Polizei wieder bei der Aufklärung eines schwierigen Mordfalls. Nachdem er den Tatort untersucht und die Zeugen befragt hat, wird ihm schnell klar, wer der Mörder. Er führt nun in gewohnter Form aus:
„Wenn Herr Kirigaya nicht der Täter ist, dann ereignete sich der Mordfall 5km von Herrn Kirigayas Wohnung entfernt. Entweder hat der Mordfall nicht 5km von Herrn Kirigayas Wohnung stattgefunden oder Frau Takahashi hat die Schreie des Opfers gehört. Wenn Herr Kirigaya sich vor der Tatzeit nicht in einem Love Hotel aufgehalten hat, dann hat Frau Takahashi die Schreie des Opfers nicht gehört. Wenn Herr Kirigaya sich vor der Tatzeit in dem Love Hotel befunden hat, dann ereignete sich der Mord auch 5km von seiner Wohnung entfernt und der Täter hätte die Halskette des Opfers gestohlen. Aber, wie Sie sehen, wurde die Halskette nicht gestohlen! Das Opfer trägt Sie immer noch. Damit sind Sie der Täter, Herr Kirigaya!“
Wie kommt Shinichi auf diese Schlussfolgerung? Ist der Täter damit überführt?
3. Aussagenlogik
Um die einzelnen Schritte in Shinichis Beweisführung logisch nachvollziehen zu können, benötigen wir Grundkenntnisse in der Aussagenlogik. Wir beschränken uns dabei auf die Aspekte, die für das Verständnis von elementarer Bedeutung sind, da durch eine allumfassende Einführung der Fokus auf den Fall verlorengehen würde.
Definition 3.1: Aussage
Eine Aussage ist ein sprachliches Gebilde, dem man auf sinnvolle Weise einen Wahrheitswert zuordnen kann. Als Wahrheitswerte kommen nur „wahr“ (\(1\)) oder „falsch“ (\(0\)) infrage.
Beispiel:
\(A_1:=\) Mein Name ist Shinichi Kudo.
\(A_2:=\) Der Mord ereignete sich im Beika-Viertel.
\(A_3:=1+1=42\)
Bei den Aussagen \(A_1\) und \(A_2\) kommt es auf die Situation an, ob sie wahr oder falsch sind (wichtig ist hier nur, dass die Aussagen entweder wahr oder falsch sind). \(A_3\) ist offensichtlich eine falsche Aussage.
Die folgenden Äußerungen sind keine Aussagen, da man ihnen keinen Wahrheitswert zuordnen kann.
\(A_4:=\) Magst Du Mathe auch so sehr wie ich?
\(A_5:=\) Hilfst Du mir bitte beim Kochen?
\(A_6:=\) Hallo Welt.
\(A_7:=\) Reiche mir das Wasser!
Die Antwort auf eine Frage ist kein Wahrheitswert. Eine Frage ist niemals eine Aussage. Genauso kann eine Aufforderung (in der Deutschen Sprache meist durch ein Ausrufezeichen am Satzende gekennzeichnet) ebenfalls keine Aussage sein.
Definition 3.2: Prämisse
Eine Prämisse ist eine Aussage, die vor dem logischen Operator \(\Longrightarrow\) (Implikation, dazu später mehr) steht. Eine Aussage, die auf der rechten Seite des Implikationspfeils steht, nennen wir Schlussfolgerung.
Beispiel:
Für \(A\Longrightarrow B\) ist \(A\) die Prämisse und \(B\) die Schlussfolgerung.
4. Logische Verknüpfungen
Man kann Aussagen mit logischen Operatoren zu komplexeren Aussagen verknüpfen.
Definition 4.1: Negation
Sei \(A\) eine Aussage. Die Negation \(\neg A\) von \(A\) (in Worten: „nicht \(A\)“) ist genau dann wahr, wenn \(A\) selbst falsch ist und genau dann falsch, wenn \(A\) selbst wahr ist.
Die dazugehörige Wahrheitstafel sieht folgendermaßen aus:
\begin{array}{|c|c|} \hline A & \neg A\\\hline 0 & 1\\\hline 1 &0\\\hline \end{array}
Wichtig:
Die Negation der Aussage „\(\pi\) ist gerade“ lautet nicht „\(\pi\) ist ungerade“, da beide Aussagen sonst falsch wären. Das ist ein häufig gemachter Fehler! Wenn z.B. etwas nicht schwarz ist, dann ist es nicht automatisch weiß. Es könnte auch violett, orange, blau oder irgendeine andere Farbe im sichtbaren Farbspektrum des menschlichen Auges sein. Das umgangssprachliche Gegenteil ist in den meisten Fällen etwas anderes als die logische Verneinung.
Definition 4.2: Konjunktion
Seien \(A\) und \(B\) Aussagen. Die Konjunktion \(A\wedge B\) von \(A\) und \(B\) (in Worten: „\(A\) und \(B\)“) ist genau dann wahr, wenn \(A\) und \(B\) beide wahr sind. Ansonsten ist die Aussage falsch.
Die dazugehörige Wahrheitstafel sieht folgendermaßen aus:
\begin{array}{|c|c|c|} \hline A & B & A\wedge B\\\hline 0 & 0 & 0 \\\hline 0 & 1 & 0 \\\hline 1 & 0 & 0 \\\hline 1 & 1 & 1 \\\hline \end{array}
Definition 4.3: Disjunktion
Seien \(A\) und \(B\) Aussagen. Die Disjunktion \(A\vee B\) von \(A\) und \(B\) (in Worten: „\(A\) oder \(B\)“) ist genau dann wahr, wenn \(A\) oder \(B\) oder beide wahr sind. Ansonsten ist die Aussage falsch.
Die dazugehörige Wahrheitstafel sieht folgendermaßen aus:
\begin{array}{|c|c|c|} \hline A & B & A\vee B\\\hline 0 & 0 & 0 \\\hline 0 & 1 & 1 \\\hline 1 & 0 & 1 \\\hline 1 & 1 & 1 \\\hline \end{array}
Umgangssprachlich meinen wir mit „oder“ meist „entweder ... oder“. Die Disjunktion entspricht dem Milch-oder-Zucker-Oder. Wenn man in einem Restaurant Kaffee bestellt, bekommt man meist die Frage „Wollen Sie Milch oder Zucker in Ihren Kaffee?“ gestellt. Man wird jedoch nicht schief angeschaut, wenn man beides nimmt. Dieses Oder ist also nicht kontravalent.
Anders ist das Exklusiv-Oder (XOR) zu interpretieren. Übertragen wir das XOR auf die Situation in einem Restaurant, so hat dies zur Folge, dass man sich z.B. bei einem Menü-Angebot, in dem ein Getränk (Cola oder Wasser) enthalten ist, für eines entscheiden muss. Wird hier „Cola oder Wasser?“ gefragt, meint man auch entweder Cola oder Wasser (nicht beides!).
Definition 4.4: Implikation
Seien \(A\) und \(B\) Aussagen. Unter der Implikation von \(A\) und \(B\) versteht man die Aussage \(A\Longrightarrow B\) (in Worten: „\(A\) impliziert \(B\)“ oder „aus \(A\) folgt \(B\)“ oder „wenn \(A\), dann \(B\)“). Dabei nennen wir \(A\) die Prämisse und \(B\) die Folgerung. Eine Implikation ist nur dann falsch, wenn die Prämisse wahr und die Folgerung falsch ist. Aus einer falschen Prämisse darf alles (auch Falsches) gefolgert werden und die Aussage ist immer noch wahr.
Die dazugehörige Wahrheitstafel sieht folgendermaßen aus:
\begin{array}{|c|c|c|} \hline A & B & A\Longrightarrow B\\\hline 0 & 0 & 1 \\\hline 0 & 1 & 1 \\\hline 1 & 0 & 0 \\\hline 1 & 1 & 1 \\\hline \end{array}
Definition 4.5: Äquivalenz
Seien \(A\) und \(B\) Aussagen. Unter der Äquivalenz von \(A\) und \(B\) versteht man die Aussage \(A\Longleftrightarrow B\) (in Worten: „\(A\) gilt genau dann, wenn \(B\) gilt“). Diese ist genau dann wahr, wenn \(A\Longrightarrow B\wedge B\Longrightarrow A\) wahr ist.
Die dazugehörige Wahrheitstafel sieht folgendermaßen aus:
\begin{array}{|c|c|c|} \hline A & B & A\Longleftrightarrow B\\\hline 0 & 0 & 1 \\\hline 0 & 1 & 0 \\\hline 1 & 0 & 0 \\\hline 1 & 1 & 1 \\\hline \end{array}
5. Operatorrangfolge
Bei der Verwendung mehrerer Operatoren in einem Ausdruck muss eindeutig entscheidbar sein, welche Bestandteile zuerst evaluiert werden. Eine der ersten Rechenregeln, die man in der Grundschule lernt, lautet „Punktrechnung vor Strichrechnung“. Hierbei handelt es sich um die Festlegung einer Operatorrangfolge, nach welcher der Operator \(\cdot\) stärker bindet als \(+\) oder \(-\). Möchte man hingegen \((40+41)\cdot 42\) ausrechnen, würde man zunächst die Summe \(40+41\) berechnen und anschließend mit \(42\) multiplizieren, was daran liegt, dass Klammern wiederum stärker als der Operator \(\cdot\) binden. Ist man sich bezüglich der Bindungsstärken unsicher, ist es nicht verkehrt durch Klammern klar zu machen, was man meint. Möchte man \(40+41\cdot 42\) ausrechnen, so sind die Klammern \(40+(41\cdot 42)\) zwar überflüssig, aber nicht falsch.
Auch in der Aussagenlogik unterliegen die Operatoren unterschiedlichen Bindungsstärken. Wir einigen uns auf folgende Operatorrangfolge:
Bemerkung 5.1: Operatorranfolge
1. \(\neg\) bindet stärker als \(\wedge\).
2. \(\wedge\) bindet stärker als \(\vee\).
3. \(\vee\) bindet stärker als \(\Longrightarrow\).
4. \(\Longrightarrow\) bindet stärker als \(\Longleftrightarrow\).
6. Äquivalenzregeln der Aussagenlogik
Es gibt eine Vielzahl an logischen Äquivalenzregeln, die einem die Arbeit mit Aussagen erleichtern. Die für unseren Fall wichtigen sind im Folgenden aufgeführt:
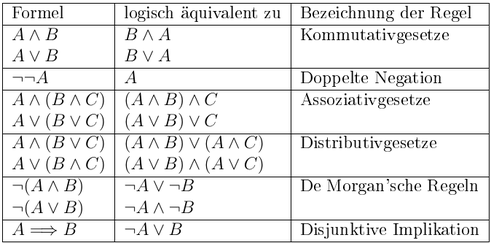
7. Ableitungsregeln der Aussagenlogik
Die folgende Übersicht listet Schlussfolgerungen auf, die man aus einfachen Formeln ziehen kann. Diese nutzt Shinichi, um Herrn Kirigaya als Täter zu entlarven.

Das war das Theoriekapitel. Im nächsten Teil (https://www.mathelounge.de/507799/mathe-artikel-001-kombinieren-wie-ein-meisterdetektiv-teil) kümmern wir uns um die Anwendung unserer Erkenntnisse auf den Fall.
Den Artikel gibt es auch auf: https://www.informatik.academy/aussagenlogik-kombinieren-wie-ein-meisterdetektiv/ (inklusive PDF-Download).
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.