Fortsetzung
Schritt 4 Extrema => g'(x)=0 setzen -> alle xE fiden, für die dies gilt: Extrema bei (xE|g(xE))
g'(x)=0
Erneut wird hier die Polynomdivision gebraucht(,da Funktion 4. Grades) (x-2) weiterhin verwendbar

0=-8/5x²+7x-18/5|:-8/5
0=x²-35/8x+9/4
*pq-Formel*
0=-p/2±√(p/2)²-q
x1 = 3.779
x2 = 0.595
Nun in die erste Funktion einsetzen für die y-Werte: (3,779|3,449) u. (0,595|1,834)
An diesen Punkten ist ein Extrempunkt. Handelt es sich um einen Hochpunkt oder Tiefpunkt?
Durch das Einsetzen von den x-Werten in g''(x) erhält man einen Wert. Wenn dieser größer als 0 ist, hat man es mit einem Tiefpunkt zu tun. Ein Hochpunkt liegt dann vor, wenn der Wert unter 0 ist. Hierbei sind beide Hochpunkte
Da die erste Ableitung für die Extremwerte zuständig ist( vgl. Extremalaufgabe), muss diese mit Null gleichgesetzt werden
Schritt 5 Wendepunkte => g''(x)=0 setzen -> alle xw finden, für die dies gilt -> Wendepunkt bei (xw|g(xw))
g''(x)=0
Auch hier verwenden wir die p-q Formel
*pq-Formel*
0=-p/2±√(p/2)²-q
x1=3,05
x2=1,2
Nun in die erste Funktion einsetzen für die y-Werte: (3,05|1,95) u. (1,2|1)
An diesen Punkten ist ein Wendepunkt. Handelt es sich um einen Rechts-Links oder Links-Rechts Wendepunkt?
Durch das Einsetzen von den x-Werten in g'''(x) erhält man einen Wert. Wenn dieser größer als 0 ist, handelt es sich um einen Rechts- Links Wendepunkt. Ist dieser jedoch kleiner als 0 --> Links-Rechts
Besonderer Wendepunkt:
falls g'(x)=0 und g(''x)=0 und g'''(x)≠0 dann nennt man diesen Sattelpunkt
Schritt 6 Symmetrie =>g(-x) betrachten
g(-x)=g(x) -->Achsensymmetrie
g(-x)=-g(x) --> Punktsymmetrie
Anhand des Grades der Funktion kann auch auf die Symmetrie gekommen werden.
Schritt 7 Zeichnen falls benötigt kann man mit der Hilfe der errechneten Punkte leichter einen Funktionsgraphen zeichnen.
Schritt 8 Deuten
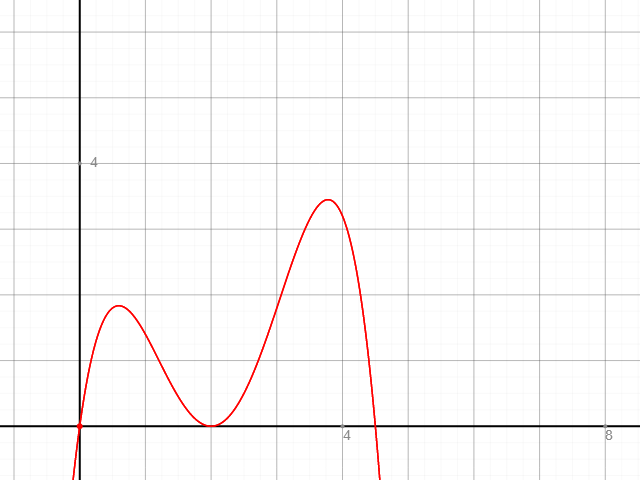
Wenn wir uns nun erneut den Graphen anschauen, so sehen wir, dass alle Punkte übereinstimmen
Hier zur Anschauung die errechneten Punkte
Nullstellen (0|0) (2|0) (4,5|0) (Lineafaktorschreibweise: (x-0)*(x-2)*(x-4,5))
Extrema (3,779|3,449) u. (0,595|1,834)
Wendepunkte (3,05|1,95) u. (1,2|1)
(Links-rechts) (Rechts-links)
Die gegebene Funktion beschreibt ja die Niederschlagsmenge. Durch die gesammelten Infos können wir jetzt einiges über die nächtlichen Schauer sagen:
Bei den Nullstellen war der Regen im kaum Messbaren
Die Höhepunkte zeigen uns wann es wirklich stark vom Himmel strömte (höchster Punkt des Intervalls)
Wendepunkte weisen uns darauf hin, dass es ein Zeitpunkt der schnellsten Geschwindigkeit ist oder in diesem Beispiel eben das rascheste Abnehmen des Niederschlags.
Diese Funktion kann auch als Widerspieglung für Die Höhe eines Heißluftballons während einer Fahrt gesehen werden oder für die Konzentration eines Medikaments im Blut.
Wenn ihr Ideen habt, könnt ihr in den Kommentaren weitere Anwendungsgebiete für die Funktion angeben und was bei den errechneten Punkten geschieht
Bei Fragen und Verbesserungsvorschlägen bitte sofort melden.
Gruß Luis