"Och man, wofür braucht man das denn später.."
So lautete bei mir im Unterricht die Reaktion mancher Mitschüler im Bezug auf das Thema Kurvendiskussion. Viele sagen, man bräuchte Mathematik kaum im späteren Leben. Hier möchte ich zeigen:
•Wofür man die Untersuchung von Funktionen benötigt
•Wie man die "wichtigen Punkte" (dazu später) deutet
•Wie man eine komplette Kurvendiskussion durchführt
[Grundlagen sind:
Ableitungen bilden; Polynomdivision/Hornerschema; p-q- Formel; Substitution; Auflösen von Gleichungen]
1.) Was soll eine Kurvendiskussion?
"Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen geometrische Eigenschaften, wie zum Beispiel Schnittpunkte mit den Koordinatenachsen, Hoch- und Tiefpunkte, Wendepunkte und gegebenenfalls noch Sattelpunkte." laut Wikipedia.
Anders ausgedrückt: Durch Berechnung von Punkten, die auf dem Graphen liegen, kann man Informationen über diese herausfinden und mit ihnen den Graphen interpretieren/deuten.
Damit sind wir bei Punkt 2
2.) Was mach ich nachdem ich die Punkte berechnet habe.(siehe unten) + 3.) Wie führe ich die Kurvendiskussion überhaupt durch?
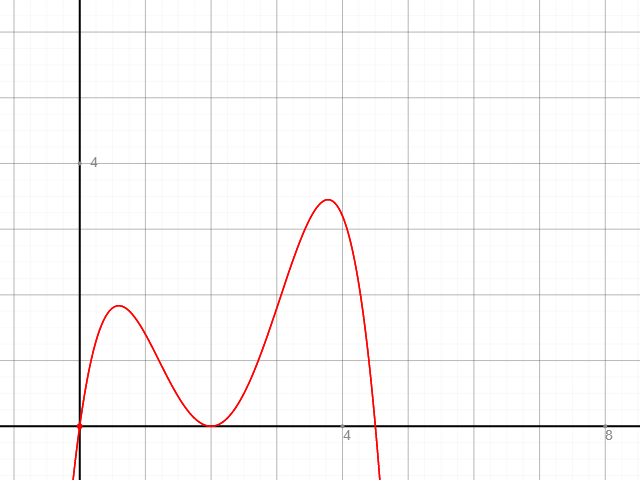
$$ g(x)=\quad -\frac { 2 }{ 5 } { x }^{ 4 }+\frac { 17 }{ 5 } { x }^{ 3 }-\frac { 44 }{ 5 } { x }^{ 2 }+\frac { 36 }{ 5 } x $$
"Diese Funktion und deren Graph spiegelt die Aufzeichnungen einer Wetterstation während einer regnerischen Nacht wieder. Die x Achse steht für die Zeit in Stunden und g(x) gibt die gemessene Niederschlagsmenge in mm/m² an."
Von dieser Funktion werden nun 3. Ableitungen gebildet (Das Ableiten ist eines der wichtigsten Teilschritte, man braucht es unbedingt):
Schritt 1 => Ableitungen bilden
g'(x)=\frac { -8 }{ 5 } x³+\frac { 51 }{ 5 } x²-\frac { 88 }{ 5 } x+\frac { 36 }{ 5 } --> Steigungsfunktion,für die Berechnung der Extremstellen
g''(x)=\frac { -24 }{ 5 } x²+\frac { 102 }{ 5 } x-\frac { 88 }{ 5 } x -->für die Berechnung der Wendepunkte
g'''(x)=\frac { -48 }{ 5 } x+\frac { 102 }{ 5 } -->für die Definierung des Wendepunkts
Schritt 2=> y=f(0) setzen ->x=0 einsetzen und y-Achsenabschnitt herausfinden
g(x)=0
g'(x)=36/5
g''(x)=-88/5
g'''(x)=102/5
Diese Punkte stehen für (0|y)
Schritt 3=>Nullstellen -> g(x)= 0 setzen -> alle x finden, für die dies gilt --> Nullstelle bei (Xo | g(Xo))
(Hierbei benötigt man Kenntnisse über die Polynomdivision/Hornerschema und über das Auflösen nach x im Allgemeinem)
g(x)=0
- Eine Nullstelle raten. Bsp. 2 --> in Linearfaktorschreibweise (x-2)
- Nun Mithilfe der Polynomdivision/Hornerschema andere Nullstellen finden

Nun haben wir eine weiter Funktion erhalten. Diese ist immer noch nicht dazu geeignet die p-q Formel anzuwenden.
Daher erneut die Polynomdivision/Hornerschema benutzen. Die erratene Nullstelle (x-2) kann weiter verwendet werden.

0=-2/5x²+9/5x ist prima geeignet die pq-Formel anzuwenden, jedoch muss zuerst durch -2/5 geteilt werden, um das x² alleine stehen zu lassen.
0=-2/5x²+9/5x |:-2/5
0=x²-4,5x
*pq-Formel*
0=-p/2±√(p/2)²-q
Man erhält als x1=0. (Durch Ausklammern von einem x kann dies auch begründet werden.)
Dies in die Grundfunktion einsetzen--> (0|0) vgl. Abbildung 1
x²-4,5x=0 kann auch umgestellt werden
x²-4,5x=0 |+4,5x
x²=4,5x |:x
x2=4,5 -->(4,5|0)
Nullstellen sagen, wo der Graph die x-Achse schneidet. Durch Gleichsetzen von g(x) mit Null wird dies erreicht
Teil 2 hier: https://www.mathelounge.de/206913/mathe-artikel-kurvendiskussion-crash-kurs-teil-2