Hallo Vanessa,
durch das Quadrieren der Gleichung bekommst Du im Allgemeinen mehr Ergebnisse als Lösungen für diese Gleichung existieren. Das liegt daran, dass das Minus-Zeichen auf einer der Seiten 'weg-quadriert' wird. Hier mal ein Beispiel:$$\begin{aligned} x-2 &= \sqrt x && \left|\, {}^2 \right. \\ x^2 -4x + 4 &= x \\ \implies x_1 &= 4, \quad x_2 = 1\end{aligned}$$Hier ist nur \(x=4\) eine Lösung der Ausgangsgleichung. Setzt Du \(x=1\) ein, so steht dort \(-1 = 1\), was natürlich falsch ist und erst durch das Quadrieren zur Gleichung wird.
Durch das Quadrieren erhalten wir hier$$\begin{aligned}2 \cos(x) +1&= 2\sin(x) \\ 4\cos^2(x) + 4\cos(x) + 1 &= 4\sin^2(x) \\ 4\cos^2(x) + 4\cos(x) + 1 &= 4\left( 1 - \cos^2(x) \right) \\ 8\cos^2(x) + 4\cos(x) -3 &= 0\\ \cos(x)_{1,2} &= \frac{-4 \pm \sqrt{16 + 4 \cdot 8 \cdot 3}}{2 \cdot 8} \\ &= \frac 14\left( -1 \pm \sqrt 7\right) \end{aligned}$$Nun liegen zwei Lösungen für den Cosinus vor. Das Argument des Kosinus (das \(x\)) kann aber auch zwei Werte für den gleichen Kosinuswert annehmen, da \(\cos(x)=\cos(-x)\) ist. D.h. wir haben vier Ergebnisse, von denen zwei richtig sind.
Mache die Probe mit allen vier möglichen Werten$$\begin{array}{r|rr}\cos(x)& x_{1,2}& x_{3,4}\\ \hline 0,4114& 1,1468& -1,1468\\ -0,9114& 2,7176& -2,7176\end{array}$$und man sieht, dass \(x_1 \approx 1,15\) und \(x_4 \approx 2\pi -2,72 \approx 3,57\) die Lösungen der Gleichung sind.
Auf Basis von \(\sin(x) - \cos(x)= 0,5\) kann man die Gleichung auch zeichnerisch lösen. Im ersten Fall nimmt man an, dass der \(\cos(x) \gt 0\):
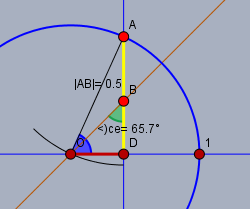
Man zeichne eine Strecke \(AB\) mit der Länge \(|AB|=0,5\) und trage bei \(B\) eine Winkel von 45° ab (grün). Der Kreis um \(A\) mit Radius 1 schneidet den Schenkel (braun) bei \(O\). Das Lot von \(O\) auf die Gerade durch \(AB\) schneidet dieselbe in \(D\). Da der Winkel \(\triangle OBD = 45°\) ist, ist das Dreieck \(\triangle ODB\) ein gleichschenkliges und somit \(|OD| = |DB|\). Folglich ist $$\begin{aligned} |AD| - |DB| &= |AB| = 0,5 \\ \underbrace{\sin\left( \angle DOA \right)}_{\text{gelb}} - \underbrace{\cos \left( \angle DOA \right)}_{\text{rot}} &= 0,5 \\ \angle DOA &\approx 65,7° \equiv 1,15\end{aligned}$$
Im zweiten Fall geht man von \(\cos(x) \lt 0\) aus. Man beginnt wieder mit der Strecke \(|AB| = 0,5\)
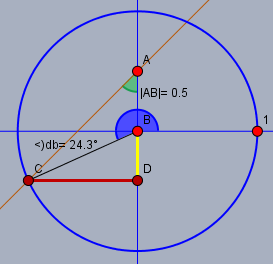
Diesmal trägt man den WInkel von 45° (grün) bei \(A\) an, dessen Schenkel (braun) von dem Kreis mit Radius \(1\) um \(B\) in \(C\) geschnitten wird. Das Lot von \(C\) auf die Gerade durch \(AB\) scheidet dieselbe in \(D\). Hier ist \(|AD| = |CD|\) da \(\triangle CDA\) gleichschenklig ist. $$\begin{aligned} -|BD| + |AD| &= 0,5 \\ \underbrace{-|\sin(\angle 1BC)|}_{\text{gelb}} + \underbrace{|\cos(\angle 1BC)|}_{\text{rot}} &= 0,5 \\ \angle 1BC &= 180° + 24,3° = 204,3° \equiv 3,57\end{aligned}$$ Gruß Werner