Hallo Sally,
A. andert sich die Größe von \(\angle AMB\), wenn sich \(C\) auf \(k\) bewegt?
Nein, siehe dazu folgende Zeichnung:
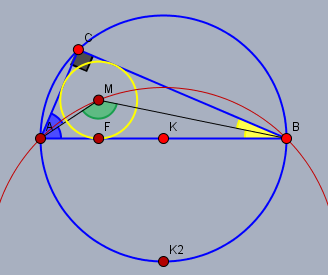
Die blauen Winkel seien \(\alpha/2\) und die gelben \(\beta/2\). Da \(\gamma\) (schwarz bei \(C\)) immer \(\pi/2\) ist, gilt$$ \begin{aligned}\alpha + \beta &= \frac {\pi}2 && |\, \div 2\\ \frac {\alpha}2 + \frac {\beta}2 &= \frac{\pi}4 = \text{konstant}\end{aligned}$$Wegen der Winkelsumme im Dreieck \(\triangle ABM\) ist \(\varphi\) (grün)$$\varphi = \pi - \left( \frac {\alpha}2 + \frac {\beta}2\right) = \frac 34 \pi \equiv 135°$$
B.) siehe (A)
C.) Ja - siehe (A)
D.) Nein - siehe (A)
Ein paar Gedanken:
- da \(\angle AMB\) konstant ist, bewegt sich \(M\) mit der Bewegung von \(C\) auf einem Kreis. Der Mittelpunkt \(K_2\) dieses Kreises liegt auf \(k\). Den Beweis dafür überlasse ich Dir ;-)
- \(C\), \(M\) und \(K_2\) liegen auf einer Geraden.
Gruß Werner