Hallo Miho,
leite die Funktion nach \(x\) und \(y\) ab: $$\begin{aligned}f(x, y) &=x^{2}-x^{2} y+y^{2} \\ \frac{\partial f}{\partial x} &= 2x- 2xy \to 0\\ \frac{\partial f}{\partial y} &= -x^2 + 2y \to 0 \implies 2y = x^2\\ 2x- x^3 &= 0 \\ x_1 &= 0, \quad x_{2,3} = \pm \sqrt 2 \end{aligned}$$der einzige x-Wert, der noch im Definitionsbereich liegt, ist \(x=0\) und \(y\) wäre dann \(y=0\). Mit der Hessematrix $$H = \begin{pmatrix} 2-2y& -2x\\ -2x& 2 \end{pmatrix}, \quad \det(H(0,0)) = 4$$folgt dann, dass es sich um ein lokales Minimum handelt. Siehe Plot:
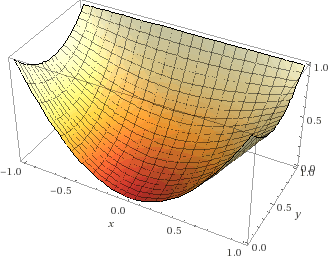
(b) kann man mittels Lagrange lösen. Am Rand \(y=0\) ist das lokale Minimum auch das auf dem Rand. Sonst gilt: minimiere \(f(x,y)\) unter der Nebenbedingung \(x^2+y^2=1\):$$\begin{aligned} L(x,y\lambda) &= x^{2}-x^{2} y+y^{2} + \lambda(x^2+y^2-1) \\ \frac{\partial L}{ \partial x } &= 2x -2xy + 2\lambda x \to 0 \implies \lambda = y-1\\ \frac{\partial L}{ \partial y } &= -x^2 + 2y + 2\lambda y \to 0 \\ -x^2 + 2y + 2y(y-1) &= 0 \\ -x^2 + 2y^2 &= 0 \end{aligned}$$Mit der Nebenbedingung folgt daraus$$\begin{aligned} -(1-y^2) + 2y^2 &= 0 \\ 3y^2 &= 1 \\ \implies y &= \frac 13 \sqrt 3, \quad x_{1,2} = \pm \frac 13 \sqrt 6\end{aligned}$$aus \(\partial L/ \partial x\) folgt noch \(x_3=0\) und \(y_3=1\) dann aus der NB ... hätte ich jetzt fast übersehen ;-)
Nachtrag zu (b):
ohne Lagrange kann man die 'Kreisform' des Randes nutzen. Ersetze \(x\) und \(y\) durch die Polarkoordinaten und man erhält:$$\begin{aligned} f(x, y) &=x^{2}-x^{2} y+y^{2} \\ x &= r \cos \varphi \\ y &= r \sin \varphi \\ f(r,\varphi) &= r^2- r^3 \cos^2 \varphi \cdot \sin \varphi, \quad \text{NB.:} \space r=1 \\ f_\varphi &= -r^3 (-2\cos \varphi \sin^2 \varphi + \cos^3\varphi ) \\ &= r^3 \cos \varphi(2 - 3\cos^2 \varphi ) \to 0\\ \implies \cos \varphi_{1,2} &= \pm \frac 13 \sqrt 6, \quad \cos \varphi_3 = 0 \end{aligned}$$der Rand \(y=0\) bleibt auch so trivial.