Hallo liebe MatheLounge Community,
ich habe folgende Aufgabe, siehe beigefügtes Bild 1… Okay, der Upload von fotografierten Buchseiten ist verboten. Also dann so:
Text erkannt:
Example: Use the Divergence Theorem to calculate the flux of \( \vec{F}(x, y, z)=\left\langle x^{3}, y^{3}, z^{3}\right\rangle \) across the sphere \( x^{2}+y^{2}+z^{2}=1 \)
The divergence of \( \vec{F} \) is
$$ \operatorname{div} \vec{F}=3 x^{2}+3 y^{2}+3 z^{2}=3\left(x^{2}+y^{2}+z^{2}\right) $$
The sphere \( S \) is the boundary of the ball \( B \) given by \( x^{2}+y^{2}+z^{2} \leq 1 . \) In spherical coordinates,
$$ B=\{(\rho, \theta, \phi) \mid 0 \leq \rho \leq 1,0 \leq \theta \leq 2 \pi, 0 \leq \phi \leq \pi\} $$
By the Divergence Theorem,
$$ \begin{aligned} \iint_{S} \vec{F} \cdot \vec{N} d S &=\iiint_{B} \operatorname{div} \vec{F} d V \\ &=3 \iiint_{B}\left(x^{2}+y^{2}+z^{2}\right) d V \\ &=3 \int \limits_{0}^{2 \pi} \int \limits_{0}^{\pi} \int \limits_{0}^{1} \rho^{4} \sin \phi d \rho d \phi d \theta \\ &=\left.\frac{6 \pi}{5} \int \limits_{0}^{\pi} \rho^{5} \sin \phi\right|_{0} ^{1} d \phi \\ &=\frac{6 \pi}{5} \int \limits_{0}^{\pi} \sin \phi d \phi \\ &=-\left.\frac{6 \pi}{5} \cos \phi\right|_{0} ^{\pi} \\ &=\frac{12 \pi}{5} \end{aligned} $$
Zu zeigen ist der Divergenz-Satz
$$ \int_{}^{}\int_{S}^{}\vec{F} \cdot \vec{N}dS=\int_{}^{}\int_{}^{}\int_{B}^{}div \vec{F} dV $$
am Beispiel
$$ \vec{F}(x,y,z)=\begin{pmatrix} x^3\\y^3\\z^3 \end{pmatrix} $$
wobei der Bereich B die Einheitskugel sein soll.
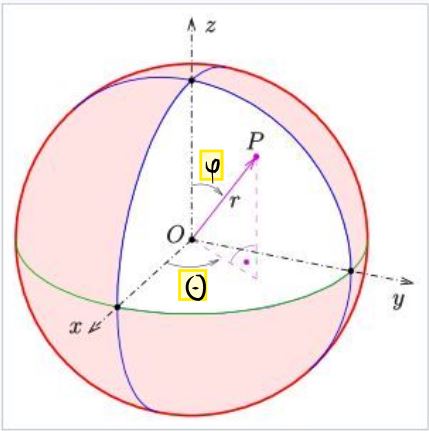
Die rechte Seite der Gleichung ergibt, wie in Bild 1 dargestellt, (12 * pi) / 5. Jetzt soll die linke Seite ausgerechnet werden. Hierfür verwenden wir die folgenden Kugelkoordinaten, gemäß dem Formalismus aus Bild 1: Siehe Wikipedia Kugelkoordinaten. Bild 2:
Berechnung von
$$ \int_{}^{}\int_{S}^{}\vec{F} \cdot \vec{N}dS $$
Das ist ein Oberflächenintegral zweiter Art.
Siehe https://de.wikipedia.org/wiki/Oberfl%C3%A4chenintegral.
Hier findet sich (Bild 3)
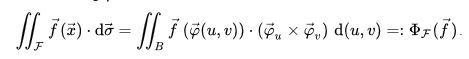
Die Parametrisierung der Oberfläche der Einheitskugel mit phi(u, v) sieht aus wie folgt, Bild 4:
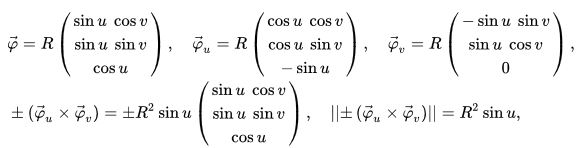
Ich habe für die u und v unser phi und theta eingesetzt, und das Doppelintegral ausgerechnet. So komme ich sowohl per Hand als auch mit dem Integralrechner,
https://www.integralrechner.de
auf 5,4265. Verschiedene Vorzeichen aufgrund der Orientierung des Normalenvektors werden hier vernachlässigt. Herauskommen muss aber (12 pi) / 5 = 7,5398. Was habe ich falsch gemacht?
Sollte es erforderlich sein, dass ich meinen gesamten Rechenweg teche, bitte Bescheid geben.
Vielen Dank!
Hier geht es um den Integralsatz von Gauß. Siehe auch Integralsatz von Stokes:
https://www.mathelounge.de/742086/integralsatz-von-stokes