Koordinatengleichungen der Tangenten bestimmen

Question

Hi zusammen :) bei folgender Frage finde ich meinen Fehler einfach nicht :( 

Tangenten des Kreises k stehen im rechten Winkel zur geraden g. Bestimme die Koordinatengleichungen  der Tangenten  k: x^2 +y^2 +16 *y = 225 , g: (x /y) = (3 / 7) +t* (-8 / 15)  . 

Als erstens habe ich k umgeformt k: x^2 + (y+8)^2 = 225  => M(0 / -8) , r=15 .

g habe ich auch umgeformt und  bekam : 15*x + 8*y -101=0  => g von der Tangente ist g: 8*x -15*y-d =0 ,

| 120- d| / 17 = ±15  => d₁ = -135 , d₂ = 375  => t₁:  8*x -15*y -135=0 , t₂: 8*x -15*y +375 =0 ..

die Antwort lautet t₁: 8*x -15*y +169=0 , t₂: 8*x -15*y - 409 =0 ?????? 

Danke euch im Voraus 

Comments

Dein Weg enthält etwas spärliche Infos zu dem, was du genau vor hast.

An sich sieht er plausibel aus. Gegen Schluss verwendest du vermutlich die HNF. 

Ich glaube du hast hier fälschlicherweise den Mittelpunkt, statt den einen Punkt auf dem Kreis eingesetzt.

| 120- d| / 17 = ±15  => d₁ = -135 , d₂ = 375  => t₁:  8*x -15*y -135=0 , t₂: 8*x -15*y +375 =0 .

Kann das sein?

---

Deine quadratische Ergänzung ist nicht korrekt. Wenn du statt y²+16y das (y+8)² schreibst, addierst du stillschweigend 8²=64. Die musst du natürlich wieder abziehen bzw. auf der anderen Seite der Gleichung wieder addieren. Dann kommst du da auf 289, so dass sich ein Radius von r = 17 ergibt.

Answer 1

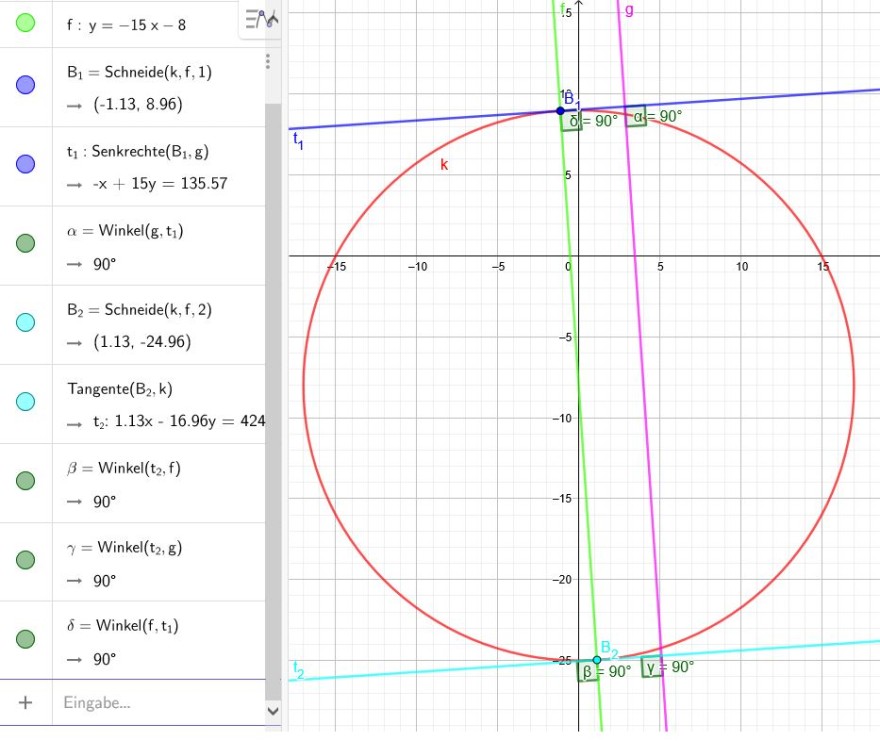
Tangenten des Kreises k stehen im rechten Winkel zur geraden g.

Bestimme die Koordinatengleichungen der Tangenten k: \(x^2 +y^2 +16 \cdot y = 225\) ,

g: \((x /y) = (3 / 7) +t \cdot (-8 / 15)\)

Umformung:

\(x=3-8t\)  Auflösung nach \(t\) :  \(8t=3-x\)       \(t=3-x\)  einsetzen in:

\(y=7+15t\)    → g:  \(y=7+15 \cdot (3-x)=52-15x\)   \(m_T=-15\)    \(m_N=\red{\frac{1}{15}}\)

 \(k(x,y)=x^2 +y^2 +16 \cdot y - 225\) 

\(k_x(x,y)=2x \)

\(k_y(x,y)=2y +16\)

\(k'(x)=-\frac{k_x(x,y)}{k_y(x,y)}=-\frac{2x}{2y +16}=-\frac{x}{y +8}\)

\(\red{\frac{1}{15}}=-\frac{x}{y +8}\)

\(y=-15x-8\)  schneidet den Kreis    k: \(x^2 +y^2 +16 \cdot y = 225\) in den beiden Berührpunkten.

\(x^2 +(-15x-8)^2 +16 \cdot (-15x-8) = 225\)

\(x_1=- \frac{17}{\sqrt{226}} \)   \(y_1=-15\cdot(- \frac{17}{\sqrt{226}})-8≈8,96\)

\(x_2= \frac{17}{\sqrt{226}} \)   \(y=-15\cdot  \frac{17}{\sqrt{226}}-8≈-24,96\)   

B_1\(( - \frac{17}{\sqrt{226}}| 8,96) \)

B_2\(( \frac{17}{\sqrt{226}}| -24,96) \)

Nun noch die beiden Tangentengleichungen aufstellen.