Wie bekomme ich epsilon raus?

Question

Hallo. Wie bekomme ich Epsilon raus?

Mit freundlichen Grüßen

Text erkannt:

a) Die Geraden AB und DC liegen parallel zueinander. Ermitteln Sie die Größe des
Winkels \( \varepsilon \)

Answer 1

Hey das ganze müsste so gehen, man kann ein GLS mit 5 Variablen aufstellen und da man 5 Gleichungen hat (die unabhängig voneinander sind) müsste man so epsilon bekommen.

Ich hoffe ich konnte dir damit helfen!

LG Simon

Comments

Kann man die Aufgabe nicht mit dem Umfangswinkel Bzw. Mittelpunkswinkelsatz berechnen?

Ich komme auf epsilon = 112 Grad..

---

Sorry ich kenn mich mit Geometrie nicht so gut aus und weiß deswegen aus dem Stehgreif nicht was du mit Umfangswinkel meinst.

Epsilon = 112 macht bei meinem GLS leider keinen Sinn, da für diesen Wert mein GLS nicht aufgeht. Entweder habe ich also einen Fehler beim aufstellen gemacht oder deine 112 Grad passen nicht. Wobei 112 nicht so viel Sinn ergibt wenn man sich das Bild mal anschaut (ich weiß dass Die Skizze nicht Maßstabsgetreu ist).

Trotzdem würde ich vermuten, dass Epsilon kleiner als 90 Grad sein müsste.

LG

---

Kann man die Aufgabe nicht mit dem Umfangswinkel Bzw. Mittelpunkswinkelsatz berechnen?

Nein - nicht mit dem Umfangswinkel, aber einfach mit Wechsel- und Stufenwinkel an Parallelen und dem Wissen, dass im gleichschenkligen Dreieck die Basiswinkel gleich sind. Z.B. im Dreieck \(\triangle ACD\). Dazu folgende Skizze:

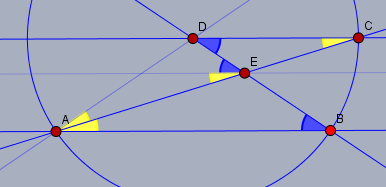
Ich habe im Punkt \(E\) noch eine weitere Parallele eingezeichnet. Alle Winkel mit gleicher Farbe sind gleich groß. Ich nenne den blauen (gegebenen) Winkel \(\alpha = 34°\) und den gelben \(\beta\). Dann ist$$\varepsilon = \alpha + \beta$$und da \(\triangle ABD\) gleichschenklig ist, gilt auch$$2 \beta = \alpha \implies \beta = \frac 12 \alpha$$Zusammen mit der ersten Gleichung folgt daraus$$\varepsilon = \alpha + \frac 12 \alpha = \frac 32 \alpha = 51°$$falls was nicht klar ist, so melde Dich bitte.

---

Vielen Dank!!!!

---

Nein - nicht mit dem Umfangswinkel

Doch, und dann ist    β = ∠BAC = 1/2 ∠BDC = α/2

Answer 2

Die Aufgabe lässt sich nicht lösen, so lange nicht alle Voraussetzungen auf den Tisch gelegt werden.

Sollte da nicht irgendwann mal die unbedeutende Tatsache genannt werden, dass D (möglicherweise) der Mittelpunkt des skizzierten Kreises sein soll?

*kopfschüttel*

Dass Fragestellern diesbezügllich der nötige Durchblick fehlt ist irgendwie verständlich, aber die anderen Beteiligten ...

Comments

Naja bei der Zeichnung die hier hochgeladen wurde handelt es sich um eine Skizze aus der man entnehmen kann, dass D den Mittelpunkt des Kreises darstellen soll.

Wenn man in so einer Situation schon aufgibt und sagt man kann die Aufgabe nicht lösen nur weil man nicht in der Lage ist eine Skizze zu deuten dann kann ich nur eins zurückgeben:

*kopfschüttel*