Aussagen zu Untervektorraum

Question

Folgendes sei gegeben:

Es sei V ein K-Vektorraum und U,W Untervektorräume von V.

Kann mir jemand sagen wieso folgende Aussage falsch ist:

Ist dim U + dim W = dim V, dann ist V = U ⊕ W.

Danke schon mal im Voraus!

Answer 1

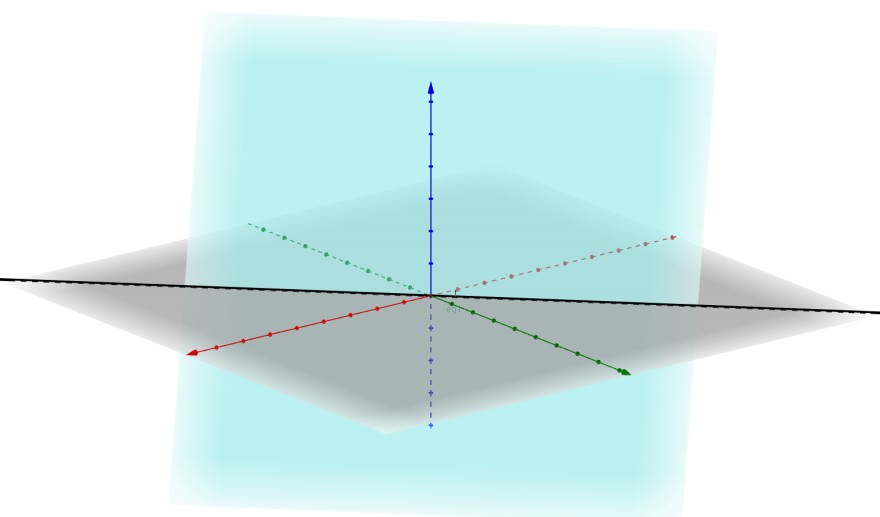
Betrachte \(V=\mathbb{R}^3\), \(U=\{(x,y,z)\in \mathbb{R}^3 : x+y+z=0\}\) und \(W=\{t\cdot (-1,1,0): t\in \mathbb{R}\}\). Die Hyperebene hat die Dimension 2, die Gerade die Dimension 1. Insgesamt also die Dimension des Anschauungsraums. Allerdings ist ihre Summe nicht direkt, denn sie besitzten offensichtlich (vgl. Bild) nicht den trivialen Schnitt. Die Gerade ist vollständig in der Ebene enthalten.