Für alle, die die Vielfalt der Mathematik kennen und nicht nur die "Pflichtaufgaben der Schule" stur abarbeiten,
möchte ich daran erinnern, dass jede endliche Zahlenfolge durch UNENDLICH viele Bildungsvorschriften (Algorithmen) konstruiert werden kann.
Am Beispiel von Aufgabe c) 16,-8,4,-2,1 hier mal 6 Algorithmen: {Hinweis: x^y = pow(x,y) }
1) pow(-1,i+1)*pow(2,5-i); in Worten:
wechselndes Vorzeichen bei der um 5 verschobenen 2er-Potenzfolge in negierter Richtung
2) "Interpolationspolynom" siehe Wikipedia: 211+3*x*(3*x*(169+x*(3*x-38))-922)/8
3) bekannte oeis-Zahlenfolge etwas umgestellt:
(-1)^(n + 1) floor((10^((n - 11)^2) (-1 + 10^(11 - n)))/(1 - 2^(56 - 5 n) 5^(55 - 5 n) + 10^(66 - 6 n))) mod 10^(10-n)
{-31, 16, -8, 4, -2, 1, -1, 0, 0}
4) Table[DivisorSigma[0, (6-n)!]*(-1)^(n+1), {n, 0, 8}] ergibt {-30, 16, -8, 4, -2, 1, -1, ...}
"Anzahl der Divisoren von der Fakultätsfunktion rückwärts mit wechselndem Vorzeichen"
5) Trigonometrische Interpolation {kann ich bei Bedarf mal vorrechnen}
6) Nachkommastellen-Algorithmus: je 2 Ziffern von (16*PI)/65-1626/(845*PI) mit wechselndem Vorzeichen
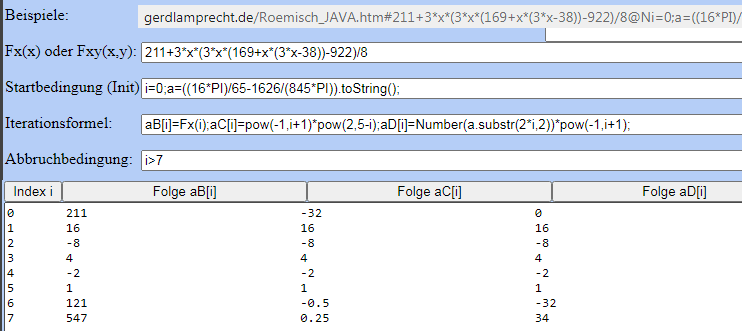
Algor. 1,2 und 6 kann der Iterationsrechner mit 1 Klick online vorrechnen:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#211+3*x*(3*x*(169+x*(3*x-38))-922)/8@Ni=0;a=((16*PI)/65-1626/(845*PI)).toString();@N@Bi]=Fx(i);@Ci]=@P-1,i+1)*@P2,5-i);aD[i]=@Ua.substr(2*i,2))*@P-1,i+1);@Ni%3E7@N0@N0@N#
...
Man kann immer so weitermachen, denn die Mathematik ist GRENZENLOS!