Aufgabe:
e^2x-y^2×y'=4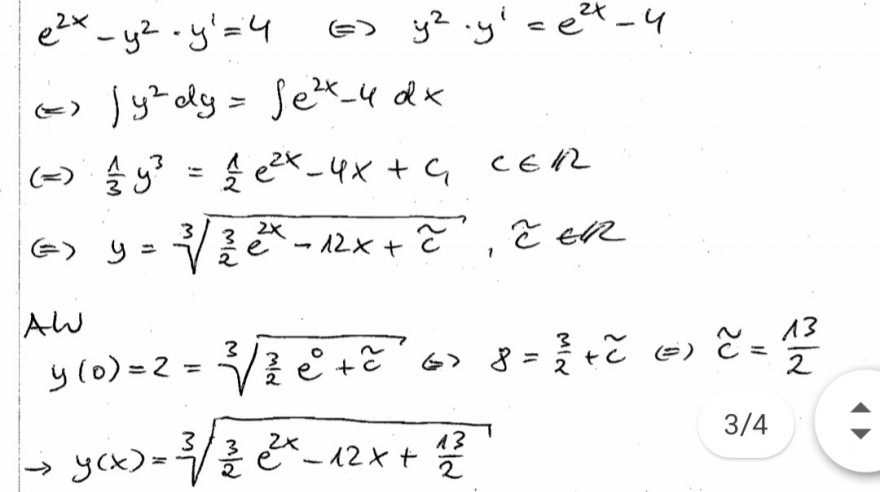
Text erkannt:
\( e^{2 x}-y^{2} \cdot y^{\prime}=4 \quad \Leftrightarrow \quad y^{2} \cdot y^{\prime}=e^{2 x}-4 \)
\( \Leftrightarrow \int y^{2} d y=\int e^{2 x}-4 d x \)
\( \Leftrightarrow \quad \frac{1}{3} y^{3}=\frac{1}{2} e^{2 x}-4 x+c_{1} \quad c \in 12 \)
\( \Leftrightarrow y=\sqrt[3]{\frac{3}{2} e^{2 x}-12 x+\tilde{c}}, \tilde{c} \in R \)
\( y(0)=2=\sqrt[3]{\frac{3}{2} e^{0}+\tilde{c}} \Leftrightarrow 8=\frac{3}{2}+\tilde{c} \Leftrightarrow \tilde{c}=\frac{13}{2} \)
\( \rightarrow y(x)=\sqrt[3]{\frac{3}{2} e^{2 x}-12 x+\frac{13}{2}} \)
Problem/Ansatz:
Hallo, ich habe eine Frage bei dieser Aufgabe, und zwar müsste normalerweise bei y^2 nicht das Minus mit? Also müsste es nicht Integral von -y^2 heißen?