Hallo,
Induktionsanfang ist ja klar: wenn \(n=8\), dann kann \(n\) als $$n=8 = 3x + 5y = 3 \cdot 1 + 5 \cdot 1 $$geschrieben werden. Für den Induktionsschritt kann man zwei Fälle unterscheiden.
1. Fall \(y > 0\): $$n + 1 = 3(x+2) + 5(y-1) = 3x + 5y + 6 - 5 = n + 1 \space \checkmark$$ 2. Fall \(y=0\) : hier kann man davon ausgehen, dass \(n \ge 9\) und damit \(x \ge 3\) ist$$n + 1 = 3(x-3) + 5(y+2) = 3x + 5y - 9 + 10 = n +1 \space \checkmark$$
Man kann sich das vorstellen, wie eine schiefe Ebene, die in X-Richtung mit 3 pro Längeneinheit ansteigt und in Y-Richtung mit 5 pro Längeneinheit. $$z = 3x + 5y $$Befindet man sich z.B. an der Position \((1|\, 1)\), so ist die aktuelle Höhe \(z=8\). Ich habe mal versucht das zu skizzieren:
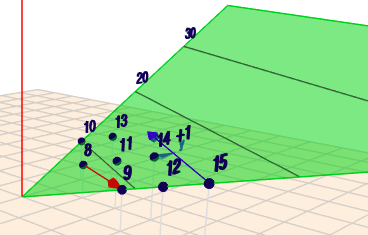
Man bewegt sich quasi in Serpentinen. Zunächst immer in Richtung \((2|\, -1)\) (rote Pfeil) solange man nicht am rechten Rand angekommen ist (bei \(y=0\)). Und von dort macht man wieder einen Schritt in Richtung \((-3|\, 2)\) (der blaue Pfeil). Die waagerechten Geraden sind die Höhenlinien bei 10, 20 und 30.
(klick auf das Bild, dann kannst Du die Szene räumlich betrachten)