In welchem Falle ist das Flächenverhältnis der beiden Rauten 3:1?

Question

Vier Höhen einer größeren Raute berenzen eine kleinere Raute (grau):

In welchem Verhältnis stehen Grundseite und Höhe der größeren Raute, wenn das Flächenverhältnis der beiden Rauten 3:1 ist?

Comments

Wenn V das Verhältnis der Flächeninhalte ist, dann ergibt sich für das gesuchte Seitenverhältnis v von Grundseite zu Höhe doch   v =  (V+1) / (2√V). Setze also V = 3  ein.

Answer 1

Hallo Roland,

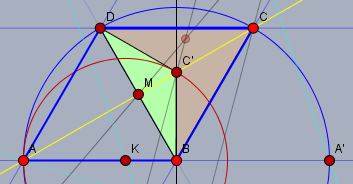
Wenn die Fläche des Dreiecks \(\triangle BC'D\) ein Drittel der Fläche des Dreiecks \(\triangle BCD\) einnehmen soll, so muss $$|MC'| = \frac 13 |MC|$$ sein. Da \(\triangle BCD\) in jedem Fall gleichschenklig ist und \(C'\) lt. Anforderung auf der Höhe des Dreiecks \(\triangle BCD\) durch \(B\) liegt, ist \(C'\) hier auch der Schwerpunkt von \(\triangle BCD\) und \(\triangle BCD\) ist somit gleichseitig.

Also ist das Verhältnis Grundseite \(|AB|=a\) zu Höhe \(h\) der größeren Raute $$\frac ah = \frac 1{\frac 12 \sqrt 3} = \frac 23 \sqrt 3$$