Stochastik unabhängigkei

Question

Aufgabe:

2. In einer groß angelegten Studie soll überprüft werden, ob der regelmäßige Konei stark zuckerhaltigen Getränken langfristig zu Diabetes führt. In einer Langzeitstudie 4385 Teilnehmern konsumierten 877 regelmäßig stark zuckerhaltige Getränke. Am Ead der Studie wurde bel 15 Personen Diabetes diagnostiziert. 20% der an Diabetes erkrank Personen waren gleichzeitig Konsumenten, die regelmäßig stark zuckerhaltige Getränke konsumierten

Problem/Ansatz:

Text erkannt:

\( k \bar{k} \)
3
12
D 874 3496 4370
\( \varepsilon(\bar{A}) \cdot 35084385 \quad P(K) \cdot P(D)= \)
\( P\left(D_{n} k\right)=\frac{15 \cdot 0,2}{4385}=3 \)
\( P(K) \cdot P(D)=\frac{817}{4385} \cdot \frac{15}{4385}=\frac{3}{4385} \)
AUfgabe 4 )

Das ist die Lösung, woher weiß ich das ich ausgerechnet diese Formel nehmen muss?

Wieso kann ich nicht einfach schreiben

P(D∩K) = 15*0,2 oder keine Ahnung was also was ist der Sinn hinter dieser Formel?

Wäre sehr dankbar für die Antwort ♡

Answer 1

Es gibt mehrere Formeln die du zur Überprüfung der Unabhängigkeit nehmen kannst

P(D und K) = P(D) * P(K)

ist nur eine davon.

Normal gilt halt immer

P(D) * P(K | D) = P(D und K) <-- Pfadmultiplikationsregel

Für die Unabhängigkeit gilt eigentlich

P(K | D) = P(K | nicht D) = P(K) <-- Formel für die Unabhängigkeit

Wenn man das also in die Formel einsetzt bekommt man

P(D) * P(K) = P(D und K)

Ich mache dir mal selber eine Vierfeldertafel mit den wichtigen Bedingten Wahrscheinlichkeiten

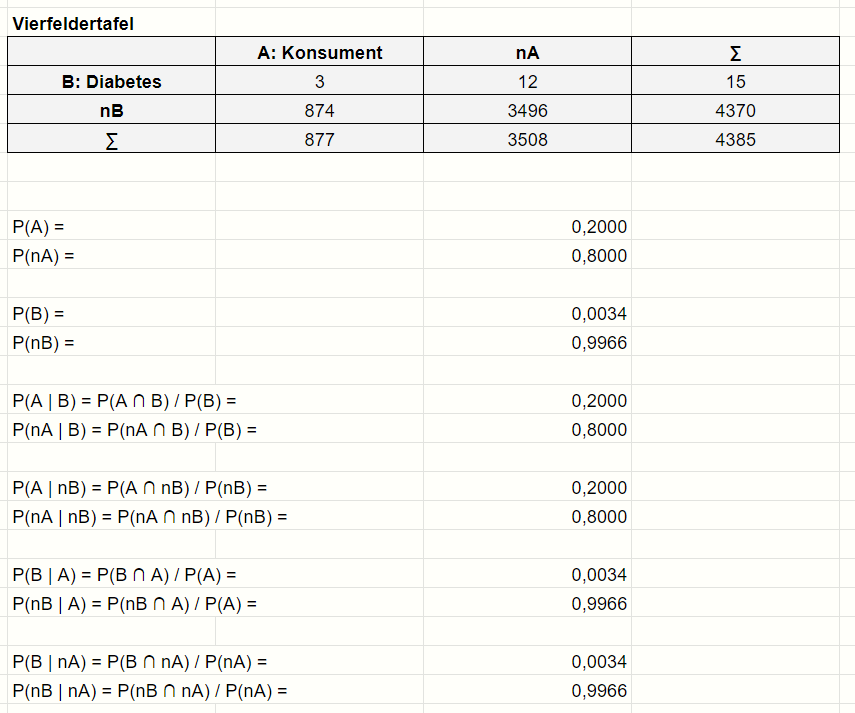
Hier siehst du prima das gilt

P(A | B) = P(A | nB) = P(A)

oder auch

P(B | A) = P(B | nA) = P(B)

Beides Formeln anhand derer man die Unabhängigkeit prüfen kann.