Gegeben ist die Strecke AB mit A=(1/5) und B=(3/-1).

Question

Aufgabe: Gegeben ist die Strecke AB mit A=(1/5) und B=(3/-1). Welche Darstellungen stimmen hier , die die Streckensymmetrale von AB beschreibt?

1) x=(2/2)+t*(2/-6)

2) x= (2/2)+t* (3/1)

3) x= (5/3) + t*(3/1)

4) x= (-2/-2) + t* (3/1)

5) x=(2/2) +t* (-6/-2)

6) 2x-2y= 16

7) 3x+y=8

8) x-3y=-4

9) 2x+2y=2

10) 9y=12+ 3x

Kann mir wer erklären welche Darstellungen hier stimmen und welche nicht ?wäre sehr nett :)

Answer 1

Hallo Lisa,

du kannst folgendermaßen vorgehen:

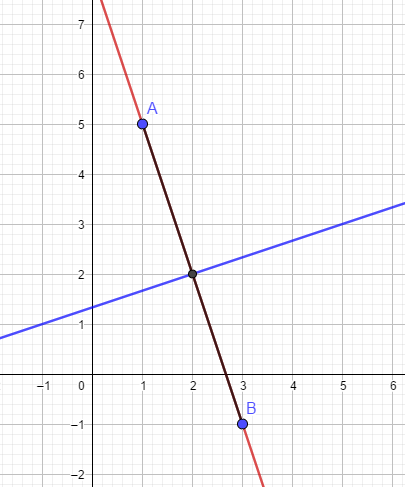
Ermittle die Koordinaten- und Parameterform der Geraden g durch A und B.

[spoiler]

$$m=\frac{5+1}{1-3}=-3\\y=-3x+b\\5=-3+b\\b=8\\[15pt] y=-3x+8\\ g:\vec{x}=\begin{pmatrix} 3\\-1 \end{pmatrix}+r\begin{pmatrix} -2\\6 \end{pmatrix}$$

[/spoiler]

Bestimme den Mittelpunkt M der Strecke von A nach B.

[spoiler]

$$M=\begin{pmatrix} 3\\-1 \end{pmatrix}+\frac{1}{2}\begin{pmatrix} -2\\6 \end{pmatrix}=\begin{pmatrix} 2\\2 \end{pmatrix}$$

[/spoiler]

Bestimme die Gleichungen der Streckensymmetrale.

[spoiler]

$$y=\frac{1}{3}x+\frac{4}{3}\\ h:\vec{x}=\begin{pmatrix} 2\\2 \end{pmatrix}+s\begin{pmatrix} -6\\-2 \end{pmatrix}$$

[/spoiler]

Wenn du dir dann zur Unterstützung noch eine Skizze machst, solltest du sagen können, welche Darstellungen stimmen.

Gruß, Silvia

Comments

Bei h muss es -2 statt -5 heißen.

Schoner fände ich noch [+6; +2] als Richtungsvektor.

:-)

---

Danke, Monty!