Dein Baumdiagramm ist doch prima.
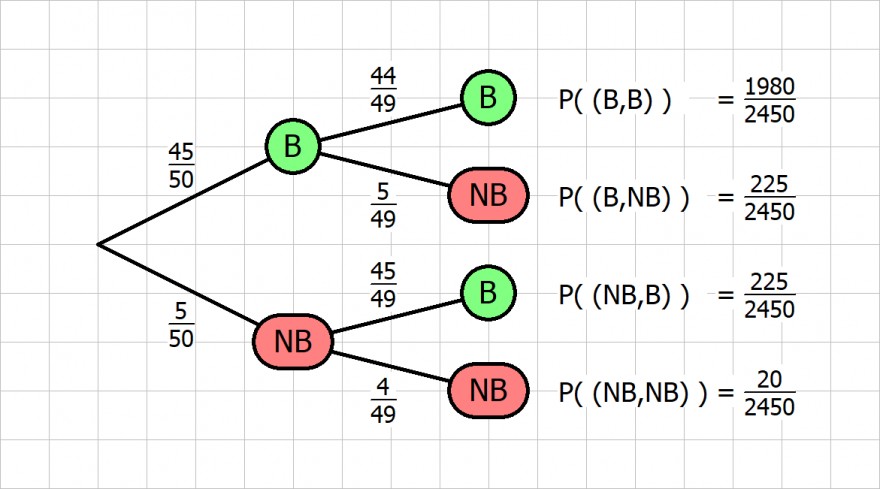
Wie groß ist die Wahrscheinlichkeit dafür, dass sie
i) beide Fragen [1980/2450 = 198/245 = 0,8082]
ii) die zweite, aber nicht die erste [225/2450 = 9/98 = 0,0918]
iii) mindestens eine Frage beantworten kann? [1 - 20/2450 = 243/245 = 0,9918]