Gegeben ist die funktion f(x) = 4x2-6x. Ermittle die Stammfunktion G(x)
$$\begin{aligned}f(x)&=4x^2-6x\\ F(x)&= \int 4x^2-6x \;dx\\ &=4\cdot \int x^2\;dx - 6\cdot \int x \;dx\\&=\frac{4x^3}{3}-3\cdot x^2 +C\end{aligned}$$ Für die Bestimmung des Wendepunkts musst du die zweite Ableitung nullsetzen und den Punkt in die dritte Ableitung einsetzen. Wenn \(f'''(x_0)\neq 0\) gilt, dann ist \(x_0\) ein Wendepunkt:
$$\begin{aligned}F''(x)&=8x-6\\ 8x-6&=0\quad &&\lvert\;\text{ Nullsetzen, } +6\\ 8x&=6\quad &&\lvert\; \div 8\\x&=3/4\implies x_0=3/4\end{aligned}$$ Dieser Wendepunkt liegt bei \(y=-1,125\), weil \(F(3/4)=-1,125\) ist. Um ihn auf \(y=1\) anzuheben, müssen wir \(C=2,125 \) wählen, damit \(2,125-1,125=1\) ist:
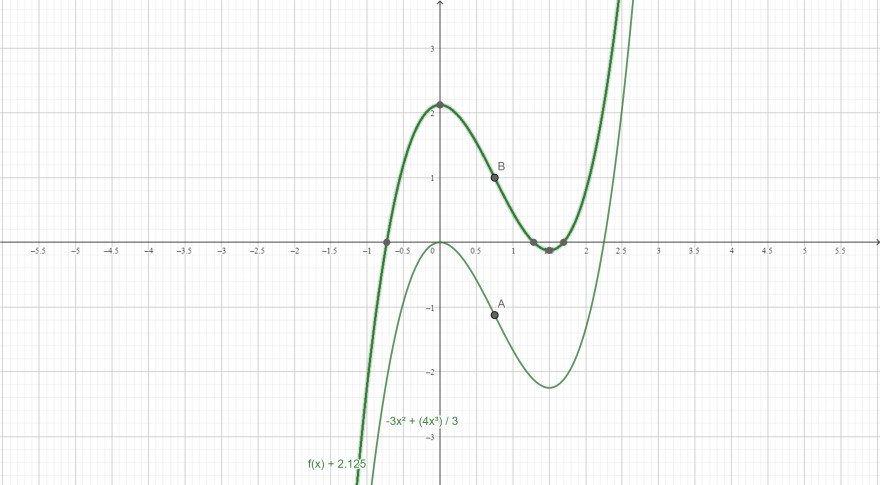
Jetzt befindet sich der Wendepunkt der Funktion \(G(x)=\frac{4x^3}{3}-3\cdot x^2 +2,125\) genau an der Stelle \(y=1\).