Hallo Anne,
a) 13 Uhr - ist richtig, wenn man annimmt, dass die Koordinaten in \(\text{km}\) angegeben sind. Obwohl es unwahrscheinlich ist, dass sich das U-Boot in 6000m Tiefe befindet!
b) 137.17° - das ist der Nebenwinkel des Winkels der Fahrtrichtungänderung. Das U-Boot bewegt sich von \(A\) nach \(B\) - folglich gilt es, den Winkel zwischen$$\vec{AB} = B-A = \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}\quad \text{und} \quad r_2 = \begin{pmatrix}-2\\ 1\\ 2\end{pmatrix}$$zu berechnen. Und das sind \(\gamma \approx 42,8°\)
c) S(-6/12/0) - ist richtig
d)zeigen sie, dass U-Boot und Dampfer auf Kurs zu einem gemeinsamen Treffpunkt sind.
Die Parameterdarstellung der Kurslinie \(d\) des Dampfers ist
$$ d: \space x(t) = D + t(I-D) \\ = \begin{pmatrix}6\\ -4\\ 0\end{pmatrix} + t \begin{pmatrix}-15\\ 20\\ 0\end{pmatrix} $$
und man kann zeigen, dass \(S\) auf \(d\) liegt. Da es für diese Gleichung$$x(t) = \begin{pmatrix}6\\ -4\\ 0\end{pmatrix} + t \begin{pmatrix}-15\\ 20\\ 0\end{pmatrix} = S = \begin{pmatrix}-6\\ 12\\ 0\end{pmatrix}$$
eine Lösung gibt. Nämlich \(t = 4/5\).
Ich habe das noch mal graphisch dargestellt:
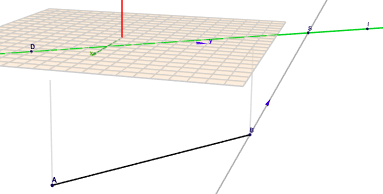
(klick auf das Bild!)
e)nein 14 Minuten Unterschied - ich habe 24min. \(|DS|=20\) - der Dampfer ist um \(14\text :00\) bei \(S\). \(|BS|=9\) und da das U-Boot um 13:00 bei \(B\) war, ist es dann um \(13\text :00 + 9/15 = 13\text:00 + 36/60= 13\text:36\) bei \(S\).
f) 12.5 km/h - ist richtig
g) 13:26 Uhr, 23,2 km - ich habe da 13:24 Uhr. Und 23km kann nicht stimmen, da das die Position kurz vorm Treffpunkt ist, und der Dampfer über 2h benötigen würde um diese Strecke zurück zu legen.
Es ist genau \(2/3\) der Zeit von 13:00 bis 13:36. Versorgungsdampfer \(d\) und U-Boot \(u\) sind um 13:24 bei $$ d(13\text: 24) = \begin{pmatrix}-2.4\\ 7.2\\ 0\end{pmatrix} \cancel{\begin{pmatrix}-4.5\\ 10\\ 0\end{pmatrix}}, \quad u(13\text: 24) = \begin{pmatrix}-4\\ 11\\ -2\end{pmatrix}$$Der Abstand ist dann ca. \( 4,58 \text{km}\space \cancel{2,29 \text{km}}\)