Woher weiß man, wann die Standardabweichung der einzelnen Messwerte einer Messreihe unterschiedlich sind?

Question

Aufgabe:

Woher weiß man, wann die Standardabweichung der einzelnen Messwerte einer Messreihe unterschiedlich sind? Oder anders gefragt, wann weiß ich, dass die jeweilige Standardabweichung zum einzelnen Messwert einer Messreihe für alle Messwerte in einer Messreihe die gleiche ist/konstant gleich bleibt?

Problem/Ansatz:

Ich würde mich sehr darüber freuen, wenn mir das jemand erklären könnte!

Comments

Hallo

misst du einen Wert n mal oder n Werte einmal. oder wie bestimmst du die Standardabweichung, das ist eigentlich die Abweichung vom Mittelwert, so dass  66% aller Messwerte  in dem Bereich um den Mittelwert liegen.

Vielleicht präzisierst du deine Frage?

lul

---

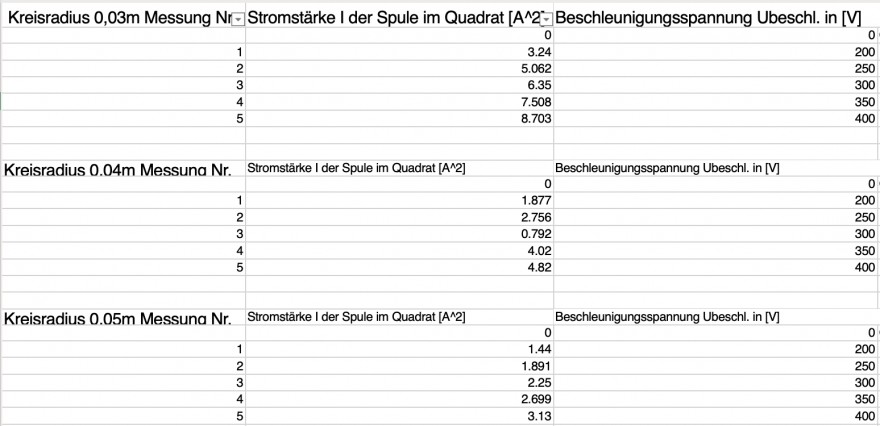
Dadurch, dass ich eine Messreihe (1) habe, die jeweils unterschiedlichen x-Werten unterschiedliche y-Werte zuordnet (also in dem Fall die Stromstärke im Quadrat und die Spannung) nehme ich mal an, dass ich n-Werte einmal messe.

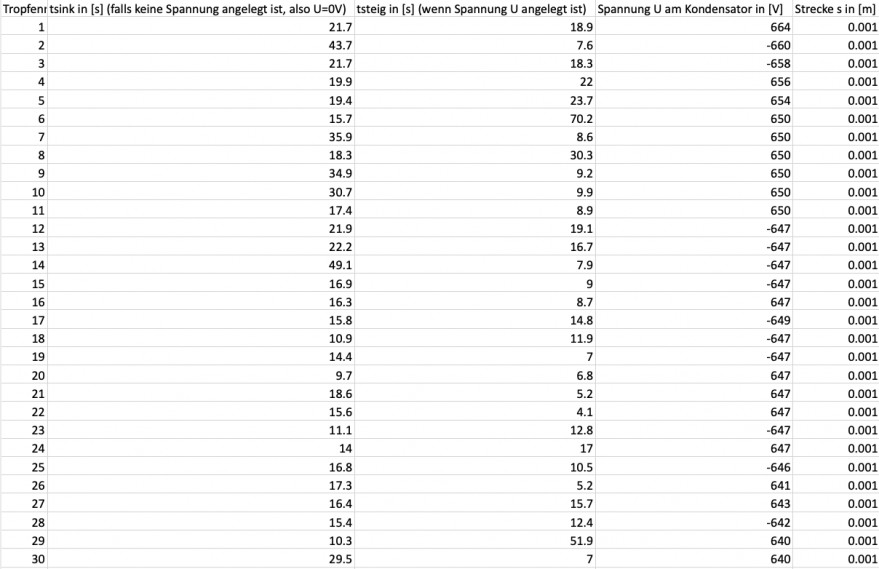
Beim Millikan-Versuch (2) habe ich n-mal einen Wert gemessen, soweit ich das richtig eingeordnet habe. Nämlich die jeweilige Sink- und Steigzeit der Tröpfchen. Dabei blieb die Strecke jeweils konstant. Nur die Spannung am Kondensator musste für das Phänomen der Tröpfchenbewegung eingestellt werden. Aber im Zentrum der Rechnung liegt die Zeit bei dieser Messreihe.

Mein Ziel ist es die Standardabweichung der Steigung a=U/I^2 der Ausgleichsgeraden zur Messreihe (1) zu finden. Die zweite Tabelle habe ich nur angefügt um sicherzugehen, dass ich das Konzept richtig verstehe. Ich habe a schon auf beide Weisen berechnet, allerdings weiß ich nicht, wann ich welchen Fall habe. Wann weiß ich, dass die jeweilige Standardabweichung zum einzelnen Messwert einer Messreihe für alle Messwerte in einer Messreihe die gleiche ist/konstant gleich bleibt?

(1)

(2)

---

Bei mir stehen 2 Formeln im Skript:

Δa=s_a=±t* \(\frac{s_y}{\sqrt{\frac{∑(x_i^2)}{s_mi^2}}}\  wenn jeder Messwert unterschiedliche Messunsicherheit besitzt

und

Δa=s_a=±t* \(\frac{s_y}{\sqrt{∑(x_i^2)}}\ bei konstanter/ gleicher Messunsicherheit für jeden Messwert

Mit s_a= Fehler der Steigung der Geraden

s_y=Maß für die Streuung der Messwerte

s_mi=Standardabweichung des Mittelwerts für den Messwert y_i

t= t-Faktor/Student Faktor =2 in dem Fall

Answer 1

Hallo Oceania, du führst den Millikan-Versuch durch. Dieser wird in https://de.wikipedia.org/wiki/Millikan-Versuch beschrieben. Du schreibst, Kreisradius 3, 4 und 5 cm. Weiter schreibst du, Stromstärke der Spule. Diese beiden Informationen passen nicht zum Millikan-Versuch gemäß Wikipedia. Bitte beschreibe uns ausführlich, welchen Versuch du durchführst, und um welche Kreise und Spulen es geht. Vielen Dank.

Comments

Oh ich habe vergessen zu erwähnen dass es sich beim ersten Versuch (Messreihe (1)) um das Fadenstrahlrohrexperiment handelt.

---

Hallo Oceania, alles klar, deine Messreihe (1) gehört zum Fadenstrahlrohr-Experiment und deine Messreihe (2) zum Millikan-Versuch. Das macht Sinn. Aber deine beiden inzwischen aufgeführten Formeln zur Berechnung von Δa, wenn jeder Messwert unterschiedliche / gleiche Unsicherheit hat, und dein Hinweis auf die Student-Verteilung, da bin ich raus, sorry.