Hallo Roland,
es folgt der Versuch eines geometrischen Beweises für das geometrische Mittel \(|AB| = \sqrt{d \cdot D}\).
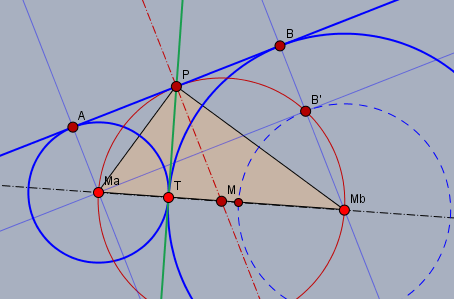
\(M_a\) und \(M_b\) seien die Mittelpunkte der beiden Kreise mit Durchmesser \(d=2r_a\) und \(D=2r_b\). Es sei \(T\) der gemeinsame Berührpunkt der Kreise und \(h\) (grün) die gemeinsame Tangente durch \(T\). \(h\) schneidet die Tangente durch \(AB\) in \(P\). Da die Vierecke \(TPAM_a\) und \(TM_bBP\) Drachenvierecke sind, ist $$|AP| = |TP| = |BP| \implies |AP| = |BP| = \frac 12 |AB|$$Der Punkt \(P\) ist also die Mitte der Strecke \(\overline{AB}\).
Die Mittelparallele \(m\) (rot gestrichelt) halbiert die Strecken \(\overline{M_aM_b}\) in \(M\) und \(\overline{AB}\) in \(P\). Da \(|MP|\) und \(|MM_a|\) jeweils das arithmetische Mittel von \(r_a\) und \(r_b\) sind, muss gelten $$|MP| = |MM_a|$$Also liegt \(P\) auch auf dem Thaleskreis (rot) über \(\overline{M_aM_b}\). Da \(h\) (grün) senkrecht auf \(\overline{M_aM_b}\) (schwarz gestrichelt) steht, ist \(T\) auch der Höhenfußpunkt von \(P\) im rechtwinkligen Dreieck \(\triangle M_aM_bP\).
Nach dem Höhensatz ist \(|TP| = \frac 12 |AB|\) das geometrische Mittel der beiden Hypotenusenabschnitte \(|M_aT| = r_a = d/2\) und \(|TM_b| = r_b = D/2\). Und damit gilt auch bei Verdoppelung der Strecken: $$|AB| = \sqrt{ d \cdot D}$$ Gruß Werner