Aufgabenstellung:
Gegeben sind die komplexen Zahlen z1 = 4 + 2i, z2 = -3 + i, z3 = -2 - 5i, z4 = 4 - 4i und z5 = 5i
Konstruiere als Punkt und Pfeil in der Gauß'schen Zahlenebene:
a) z1 + z2
b) z1 - z4
c) (z1 + z3) + z5
d) 2z2
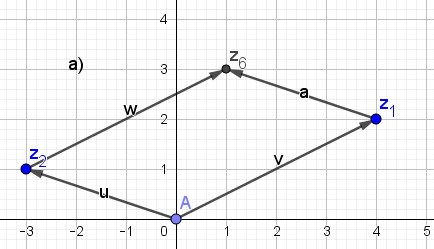
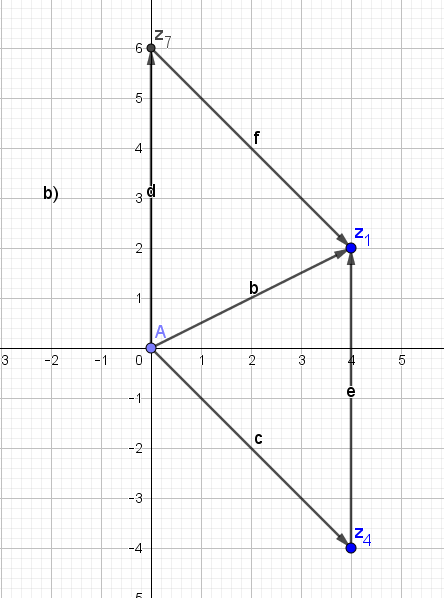
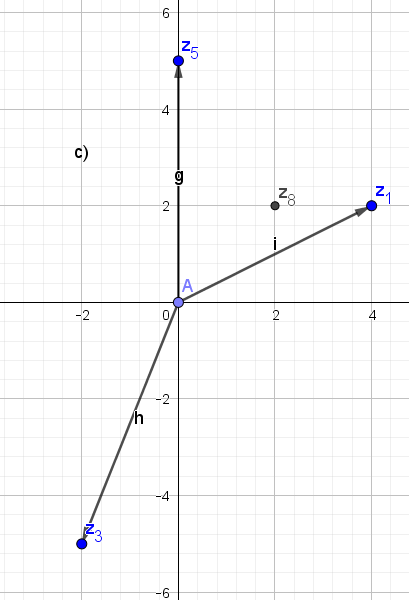

Ich bin mir bei a) und b) ziemlich unsicher ob ich es richtig angegeben habe, bei c) wusste ich nicht mehr weiter.. bei d) wiederum bin ich mir sicher... Könntet ihr mir bitte helfen?
VIelen Dank im Voraus!