1) \( (2 + i) + (-1+i) = 2-1 + i + i\ = 1 +2i\)

\((1+i) \cdot (-1+i) = 1\cdot (-1) + i\cdot i + 1 \cdot i + i \cdot (-1) = -1 + (-1) + i - i = -2\)
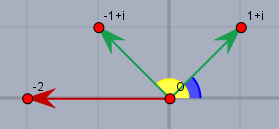
Die Beträge der beiden grünen komplexen Zahlen sind jeweils \(\sqrt{2}\). Das Ergebnis hat den Betrag \(2\). Und das Argument (der Winkel des roten Pfeils) des Ergebnisses ist die Summe aus den Winkeln der grünen Pfeile.
2) Die Multiplikation zweier komplexer Zahlen geht wie in der Algebra gewohnt: $$(a+bi)(c+di) = ac-bd + (ad + bc)i$$ alles weitere sollte dann kein Problem sein.
3) \(d= z - z_0 = 3+2i - (1+i) = 2+i\) und \(|d| = \sqrt{2^2+1^2} = \sqrt{5} < 2,5 \) also liegt \(z\) innerhalb des Kreises um \(z_0\) mit dem Radius \(r=2,5\). Wie auch folgende Skizze zeigt:
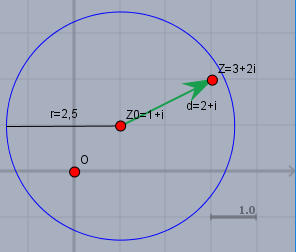
Nein - das Argument (d.h. den Winkel den \(d\) gegenüber dem reellen annimmt) braucht man dafür nicht.