Aufgabe:
Gegeben ist die komplexe Zahl \( z_{1}=1+\mathrm{i} \sqrt{3} \)
a) Berechnen Sie Betrag \( r_{1}=\left|z_{1}\right| \) und Argument \( \varphi_{1}=\arg \left(z_{1}\right) \) und geben Sie \( z_{1} \) in der Polarkoordinatendarstellung \( z_{1}=r \mathrm{e}^{\mathrm{i} \varphi} \) an
b) Berechnen Sie nun \( z_{1}^{2} \)
c) Berechnen Sie \( z_{1}+z_{2} \) und \( z_{1} \cdot z_{2} \) wobei \( z_{2}=1-\mathrm{i} \sqrt{3} \)
d) Zeichen Sie \( z_{1}, z_{2}, z_{1}+z_{2} \) und \( z_{1} \cdot z_{2} \) in die Gaußsche Zahlenebene ein.
Ansätze:
zu a)
\( 1+i \sqrt{3}=\left(\frac{1}{2}+i \frac{1}{2} \sqrt{3}\right) \)
\( \phi=0 \quad \phi=60^{\circ} \quad \phi=60^{\circ} \)
\( \phi=\frac{\pi}{3} \)
\( 2 e^{i \frac{\pi}{3}} \)
zu b) Was ist mit $${ z }_{ 2 }^{ 1 }$$ gemeint?
zu c)
\( z_{1}=1+i \sqrt{3} \)
\( z_{2}=1-i \sqrt{3} \)
\( z_{1}+z_{2}=2+0 i \)
\( z_{1} * z_{2}=3,9929+0 i \)
zu d)
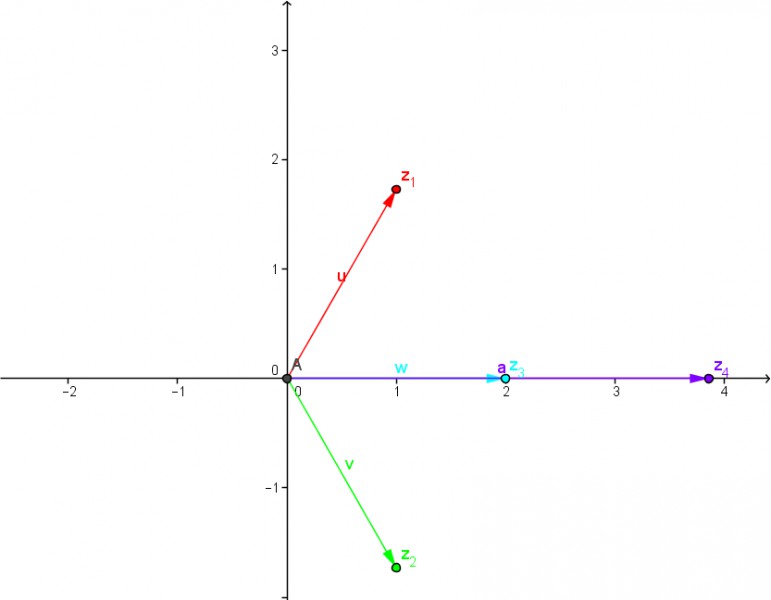
z1, z2, z1 + z2 und z1 ·z2
