Koch's Tetraederfraktal Anzahl Tetraeder pro Iterationsschritt berechnen

Question

Auf Rolands Spuren:

Das räumliche Analogon zur Koch-Kurve kann als ein Tetraederfraktal aufgefasst werden.
Die vier Seitenflächen eines regulären Tetraeders werden durch Halbieren der Kanten in vier gleichseitige Dreiecke geteilt über denen neue Tetraeder errichtet werden. Die Seitenhalbierung wird über alle Tetraeder weitergeführt. In der ersten Iterationsstufe entsteht der Kepplerstern. Die acht Ecken der Stella Octangula sind die Ecken eines Würfels. Das Tetraederfraktal (unendlich viele Halbierungen) füllt das Würfel-Volumen aus.

Gesucht eine Formel zur Berechnung der Anzahl sichtbarer Tetraeder.

Iterationsschritte durch Farben Grün, Rot, Blau, Gelb (teilweise) , Violett (Ausschnitt einer Seite)  dargestellt.

Modell

https://www.geogebra.org/m/dncckhtq

Answer 1

$$A1=1$$

$$A2=8$$

$$A3=56= 8+(2^2-2)*12$$$$+(2^1-1)^2*24$$

$$A4=296=8 +(2^3-2)*12$$$$+(2^2-1)^2*24$$

 $$n>2$$

$$An=8+(2^{(n-1)}-2)*12$$$$+(2^{(n-2)}-1)^2*24$$

Oder auch

$$n>1$$

$$An=8+(2^{(n-2)}-1)*24$$$$+(2^{(n-2)}-1)^2*24$$

http://www.math.tu-dresden.de/modellsammlung/karte.php?ID=558

Achtung, die im Link angegebenen Iterationsstufen sind um 1 anders als die hier angegebenen Folgen.

Comments

Tetraeder gezählt (hab oben noch einen Link auf ein Modell angegeben)

1 - 1

2 - 8

3 - 56

...

---

Dein A1 ist mein A0 =1

Doch dann sagst du ,bei

2 ;8  ich sage bei 1; 16

Meine 16 kommen dadurch zustande, dass ich auf 4 Flächen des Tetraeders jeweils 4 Tetraeder sehen könnte, wenn ich den Tetraeder drehen würde. Ich kann sie also nicht auf einmal sehen, sondern nacheinander.

Dann sagst du

3; 56  mein A2=kommt zustande, weil ich ja 19 Tetraeder hatte, davon 57 Flächen sehen konnte und darauf dann 57*4  =228 Tetraeder setzen konnte.

---

Ich habe meine Antwort geändert, doch momentan komme ich nicht weiter, es ist wirklich schwierig, obwohl es den Anschein hat, als ob es dann wieder einfacher wird, da die Form sich ja den Würfel anpasst.

---

Ich habe eine Verständnisfrage.

Wenn ich bei der i-ten Iteration Tetraeder dazu gefügt habe, werden die bei der i+1-ten Iteration als ein Tetraeder gezählt, oder als zwei kleinere Tetraeder?

Dazu habe ich ein kleines Bild gemalt.

Die großen Ovale sind noch der i-ten Iteration entstanden, die mittleren ausgefüllten Ovale nach der i+1 ten Iteration und die kleinen Kreise nach der i+2ten Iteration. Soll ich die Ovale erst einfach , dann doppelt und dann vierfach zählen und die ausgefüllten Ovale entsprechend einfach, dann doppelt? Oder zählen sie immer  nur einfach weil es ja auch nur ein Tetraeder ist?

Ich hoffe, dass ich mich verständlich ausgedrückt habe.

---

I’m ersten Schritt werden auf dem grünen Tet 4 rote Tets gesetzt, die den Grünen in 4 Tets  zerteilt macht 8 Tets. Hier der nächste Schritt. Auf jedem der 8 Tet werden 3 blaue angesetzt, die die vorhandenen in 4 Tet zerteilt mach 3x8+4x8=56

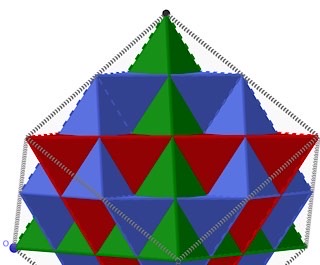
Dieser Schritt wiederholt sichin jedem Wurfelblock mit halbierten Kanten:

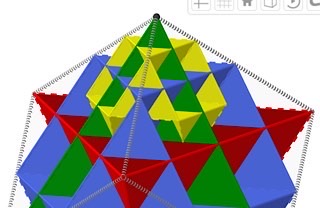
In der Draufsicht

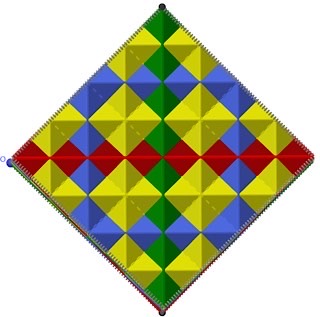
8x8 Tet auf einer Seite:Start mit grün, rote, blaue und gelbe aufgesetzt. Alle Seiten sehen identisch aus,

Siehe die App im Link für erweitere Erläuterungen und Beispiele.

Noch ein Schritt violett aufgesetzt

Die Rand-Tets sind natürlich auch von den anderen Seiten aus zu sehen, dürfen nicht doppelt gezählt werden...

---

Das war nicht meine Frage. Wenn ich die angenähert Kubusform habe, dann habe ich an den Seitenflächen ja pyramiedenförmige Trichter. Wenn ich da nun kleine Tetraeder reinlegen, teile ich meinen ursprünglichen Tetraeder an der Seite optisch in zei Teile, ich weiß  also, dass es ein Tetraeder pro Seite des Trichters war, es sieht aber aus, als wenn es einer ist.

"Auf jedem der 8 Tet werden 3 blaue angesetzt, die die vorhandenen in 4 Tet zerteilt mach 3x8+4x8=56"

Gut,  jetzt habe ich es gefunden, Obwohl der ursprüngliche Tetraeder ein Tetraeder ist, wird er optisch wie viele kleine behandelt. Also in immer kleinere Tets aufgeteilt.

---

Ich habe die Antwort überarbeitet.

Hogar

---

Hm,

welche Tetraeder willst Du denn in einem Tricher mit quadratischer Grundfläche einlegen?

Wie auch immer - Deine Überlegungen decken sich mit meinen

\(T(n)_{n≥1} =6 \cdot 2^{2n} - 12 \cdot 2^n + 8 \)

Danke fürs mit denken...

Dann werd ich das so übernehmen.

Die Nummerierung in der App werde ich ändern - mit 0 beginnen.
Mein Internet war wech - deshalb hab ich mit dem Android-Phone draufgeschaut - da läuft die App auch schön rund. Hät ich jetzt nicht unbedingt erwartet. Sind doch recht viele Objekte die sich durchdringen...

---

Ich habe mir nur eine Seite des Quaders angesehen. Deine vielen Bilder und Filme haben mich doch eher verwirrt.

Genauer habe ich nur ein Viertel des Quaders angesehen. Die Eckpunkte waren ja klar, da gab es insgesamt 8 Ecken. Der Rand musste mal 12 genommen werden, auch dort war das Bildungsgesetz schnell zu finden und dann hatte ich etwas mit der Summen Formel in die beiden Richtungen rumgespielt, in eine Richtung musste ich ja immer einen weniger nehmen, als in die andere, da ich die vier Viertel ja zu einem zusammen fassen wollte.

Danke für die Wertung und alles Gute.

Gruß, Hogar

---

Merkwürdig finde ich, dass man bei oeis.org die Folge nicht findet.

Bei 1, 8, 56, 296, wird eine andere Folge angegeben. Das hatte mich anfangs irritiert.