Verhältnisbestimmung zweier flächengleicher Dreiecke, die sich überschneiden.

Question

wir haben von unserem Lehrer über die Ferien eine aufgabe bekommen die wir lösen MÜSSEN!

ich habe mich daran versucht komme nur leider gar nicht weiter da Geometrie nur große Fragezeichen in meinen Kopf wirft... ich hoffe ihr könnt mir helfen oder zumindest einen Ansatz nennen mit dem ich es versuchen könnte..

ich habe ein gleichschenkliges Dreieck bei dem eine Kathete doppelt so lang ist wie die Basis, dieses Dreieck spiegelt man an dem innenkreismittelpunkt (ich habe die mittelsenkrechten aller drei Seiten eingezeichnet und den Schnittpunkt als innenkreismittelpunkt verwendet, ich hoffe das stimmt so) nun ist ein Sechseck entstanden, allerdings weis ich nicht wie ich den Flächeninhalt des neuen Sechsecks berechnen soll und dies ist meine Aufgabe, habt ihr einen tipp für mich?

Comments

Schnittpunkt der Mittelsenkrechten ist der Umkreismittelpunkt.

Du musst die Winkelhalbierenden benutzen. Deren Mittelpunkt ist der Mittelpunkt des Inkreises.

---

Ich bin gleich weg. Hab aber noch kurz eine Skizze gemacht. Eventuell hilft sie Dir schon weiter? Oder jemand anderem? (Natürlich gibt es vielleicht nen viel einfacheren Weg :P)

 

Meine Idee die noch ausgeführt werden muss.

a (Basis) ist bekannt. Somit auch die halbe Basis und deren Höhe.

Ebenfalls bekannt ist die Lage des Inkreises (siehe Formelsammlung um r zu berechnen).

Nun nur noch Strahlensatz anwenden um b zu errechnen.

Mit b (und man hat ja auch r) kann man c errechnen. Eventuell über den Strahlensatz übrigens auch d.

Damit bleibt nur noch e übrig zu berechnen. Außerdem e = f.

 

(Sry wenns etwas knapp ist. Bin in Eile)

 

Viel Spaß denen, die sich damit befassen.

Grüße

---

Den Winkel brauche ich ja für den Kosinus-Satz, ich weiß aber nicht wie ich diese berechne

---

Welchen Winkel?

---

hier hast du es angesprochen "Verbleibt nur noch b. Man hat ja nen rechtwinkliges Dreieck oben rechts (über die Seiten r, b und c). Damit kann man auch die restlichen Winkel bestimmen. Insbesondere den unteren. Da ein 90°-Winkel zur roten Horizontalen vorliegt kann also der Winkel z bestimmt werden. Cosinussatz anwendet und man hat e "

---

und ist der strahlensatz nicht falsch? "$$\frac ah = \frac{b}{h-2r}$$"?

---

Wir haben doch b (siehe meine eigentliche Antwort) und r ist sowieso bekannt. Dann erkennst Du ein rechtwinkliges Dreieck und alles davon ist bekannt. Hat man den Winkel zwischen r und c so kann man den Winkel zwischen c und d ausrechnen, da 90°-(Winkel zwischen r und c) = Winkel zwischen c und d ist ;).

---

Wieso soll der Strahlensatz falsch sein? Beachte, dass a der halben Basis entspricht.

---

aber woher haben wir den winkel zwischen r und c? achja die halbebasis, danke (:

---

Über trigonometrische Beziehungen.

Der Winkel sei ß,

dann ist

tan(ß) = b/r

ß = arctan(b/r)


;)

---

Gerne ;)    .

---

heißt es hier beim Strahlensatz "a*h = d/h-r" oder "a/h = d/h-r"

---

und h entspricht der höhe des kompletten Dreiecks oder? demnach kann man h berechnen mit Hilfe des Pythagoras, da ich g (Schenkel) ja aus a definiert habe, denn dann brauche ich den Schritt um b aus den Seiten r b und c gar nicht oder?

---

Beachte bitte, dass das zwei verschiedene Ansätze sind. In meinem Kommentar gehe ich leicht anders vor als in der Antwort selbst.


Und ja, es ist a/h ;). Wobei h die Höhe des Gesamtdreiecks ist.

---

aber diese frage stellt sich mir alleinein deiner antwort "Strahlensatz (a sei die halbe Basis): $$\frac ah = \frac{b}{h-2r}$$ Die einizige Unbekannte ist demnach b. . . . Verbleibt nur noch b. Man hat ja nen rechtwinkliges Dreieck oben rechts (über die Seiten r, b und c)." bei welchen schritten genau gehst du in dem Kommentar anders vor?

---

Aso jetzt sehe ich was Du meinst. Kann mich allerdings grad nimmer erinnern, warum ich das geschrieben habe bzw. den Zweck erkennen. Fehlt denn noch was, wenn man den Absatz außer Acht lässt? Man müsste ja alles berechnen können?!

---

nein, ich dachte nur, dann kann ich b gleich bestimmen und nicht am ende nochmal, weil es ja dann mehr Arbeit wäre :D

---

Weiß nicht mehr, was mich da geritten hat :D. Aber dann passt die Sache ja nun ;).

---

Was für ein Zufall - das ist die vierte Aufgabe der zweiten Runde des Landeswettbewerbs Mathematik!

Von den vier Aufgaben der zweiten Runde lassen sich 3 in diesem Forum wiederfinden...

Answer 1

Hi,

ich lege nochmals ein wenig klarer meinen Ansatz dar. Dann kannst Du weiterbasteln :).

Nochmals eine bessere Version des Bildes.

 

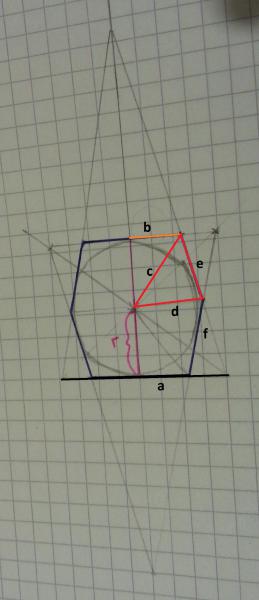
(Es sei vorausgesetzt, dass r bekannt sei http://www.mathematische-basteleien.de/gdreieck.htm )

Strahlensatz (a sei die halbe Basis):

$$\frac ah = \frac{b}{h-2r}$$

Die einizige Unbekannte ist demnach b.

Auf dieselbe Weise kann man d berechnen.

$$\frac ah = \frac{d}{h-r}$$

 

Für c hat man ein rechtwinkliges Dreieck, welches aus den Seiten r, b und c besteht:

$$c^2 = r^2+b^2$$

 

Verbleibt nur noch b. Man hat ja nen rechtwinkliges Dreieck oben rechts (über die Seiten r, b und c). Damit kann man auch die restlichen Winkel bestimmen. Insbesondere den unteren. Da ein 90°-Winkel zur roten Horizontalen vorliegt kann also der Winkel z bestimmt werden.

Cosinussatz anwendet und man hat e.

Nun hat man das Dreieck r,b und c, sowie das rote Dreieck. Die Flächeninhalte berechne und nehme das mal 4 und Du hast den Flächeninhalt des Sechsecks.

 

Grüße

Comments

danke ich kann den Lösungsweg nachvollziehen, aber leider habe ich r nicht gegeben, hast du vielleicht eine andere Idee für mich wie ich auf das Verhältnis des Flächeninhalts des Dreiecks und des Sechsecks berechnen kann wenn ich r nicht gegeben habe und somit den Flächeninhalt selbst nicht berechnen kann oder muss ich das über die variablen machen? ich steh echt auf der Leitung ...

---

Doch r kannst Du auch in Abhängigkeit von a (bzw. 2a = Basis) ausdrücken. Ich war nur zu faul (es war 2 Uhr nachts) das noch auszurechnen/hinzuschreiben und hatte auf en Link verwiesen (der jetzt auch funktioniert :P).

Alternativ findet man r übrigens auch über Heron:

r = √((s - 2a)·(s - g)·(s - g)/s)

wobei s der halbe Umfang ist, also (2a+g+g) = (2a+4a+4a) = 10a

(g sei die Länge der Schenkel und 2a die Länge der Basis. Dank dem Wissen aus der Aufgabe ist g = 4a (also das doppelte der Basis)).

---

oke ich werde es nochmal versuchen Dankeschön!! :)

---

Viel Spaß :)

---

es hat sich mir nun doch noch eine frage gestellt, welcher ist der Winkel z und wo genau finde ich hier einen 90° Winkel? ( Damit kann man auch die restlichen Winkel bestimmen. Insbesondere den unteren. Da ein 90°-Winkel zur roten Horizontalen vorliegt kann also der Winkel z bestimmt werden.)

---

Den rechten Winkel findest Du, wenn Du den oberen Teil der rosanen Linie nimmst (r) und die nach rechtslaufende rote (d).

Im rosa, rot, orangenen Dreieck (rbc) ist alles bekannt, bzw. kann errechnet werden, also auch der untere Winkel. Folglich ist dann z = 90°-genannter Winkel.


Ok? :)

---

was bedeutet das $$ bzw. das $$\frac ?

---

Wo meinst Du denn das?

Also "\frac{}{}" ist der TeX-Befehl um nen Bruch zu schreiben. In der ersten Klammer ist der Zähler einzutragen in den zweiten der Nenner.

---

und was bedeuten die Dollar zeichen?

---

und wie berechne ich die restlichen winkel im Dreieck rbc, wenn ich nur einen 90°-winkel habe, da es ja kein gleichschenkliges Dreieck ist

---

Das brauchts um den "TeX"-Code umzusetzen.


Ohne Dollar

\frac{3}{4}

Mit Dollar

$$\frac{3}{4}$$