Das Glücksrad wird 2x gedreht.
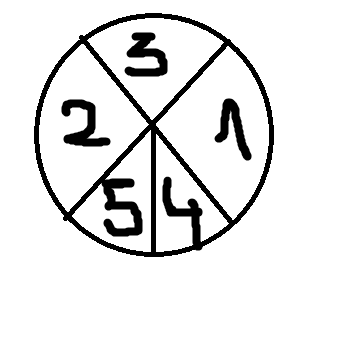
X sei der Gewinn pro Spiel.
Einsatz pro Spiel: 0.50€
Auszahlung: 10 Pkt = 4 €
9 Pkt. = 2€
8 Pkt. = 1€
a) welche Werte kann X annehmen?
Lösung: 3.5, 1.5 und 0.5
b) Bestimmen Sie die Wahrscheinlichkeitsverteilung von X als Tabelle
Lösung:
kann mir bitte jemand helfen, die Tabelle zu vollständigen?
c) ist das Spiel günstig für den Spieler?
Dafür bräuchte ich erstmal die komplette Tabelle...
:)