Hallo,
Mit der Information, dass die Parabel die lineare Funktion \(y(x) = 0,5x+4,5\) bei \(x=0\) und \(x=5\) schneidet, sind zwei Punkte der Parabel bekannt:
\(A(0;\,y(0)=4,5)\) und \(B(5; \, y(5) = 7)\). Spontan fallen mir drei verschieden Lösungen ein:
1.) da die X-Position des Scheitels gegeben ist, starte mit der Scheitelpunktform der Parabel$$p(x) = a(x-x_s)^2 + y_s$$\(x_s\) ist bereits gegeben mit \(x_s = 3\). Wenn man nun weiß, dass die Steigung der Parabel in der Mitte zwischen zwei Schnittpunkten einer Sehne identisch zur Steigung der Sehne ist, so weiß man, dass $$p'\left(x = \frac{0+5}{2} \right) = y'(x) = 0,5$$Daraus folgt dann direkt \(a\):$$p'(x) = 2a(x-x_s) \\ p'(2,5) = 2a (2,5 - 3 ) = 0,5 \implies a = -0,5$$ Und für das \(y_s\) muss man nur einen der gegebenen Punkte in \(p(x)\) einsetzen. Zum Beispiel \((5;\, 7)\):$$p(5) = -\frac 12(5 - 3)^2 + y_s= 7 \implies y_s = 9$$
2.) Ausgehend von der allgemeinen Form einer Parabel $$p(x) = ax^2 +bx + c$$ kann man auch drei Gleichungen aufstellen. Zwei für die gegebenen Punkte und die dritte für die Vorgabe, dass \(p'(3)=0\) sein muss:$$p(0) = a \cdot 0^2 +b \cdot 0 + c = 4,5 \\ p(5) = a \cdot 5^2 + b \cdot 5 + c = 7\\ p'(3) = 2a \cdot 3 + b = 0$$Das sind drei Gleichung mit den drei Unbekannten \(a\), \(b\) und \(c\) und der Lösung \(a= -0,5\), \(b=3\) und \(c=4,5\).
3.) die dritte Lösung ist rein graphisch. Du hast ja geschrieben, dass Du es schon gezeichnet hast.
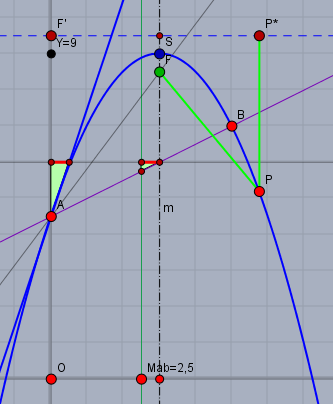
Die gegebene Gerade (lila) geht durch die Punkte \(A\) und \(B\), die auch Punkte der Parabel sind. Die Mittelachse \(m\) (schwarz Strich-Punkt) liegt bei \(x_s=3\).
Wie oben nutze ich wieder aus, dass die Steigung der Parabel in der Mitte der Strecke \(AB\) gleich der Steigung der Sehne \(AB\) ist. Dazu zeichnet man das Steigungsdreieck an \(y\) bei \(x=2,5\). Nun muss man wissen, dass die Steigung einer Parabel sich mit \(x\) linear ändert. Die Steigung bei \(x=x_s=3\) muss \(=0\) sein. Daraus konstruiere ich das Steigungsdreieck im Punkt \(A\) und damit die Tangente (blau) der Parabel im Punkt \(A\). Das Spiegelbild der Parallelen zu \(m\) durch \(A\) schneidet \(m\) im Brennpunkt \(F\). Das Spiegelbild von \(F\) an der Tangenten liegt auf der sogenannten Leitgeraden der Parabel (blau gestrichelt). Die Leitgerade steht immer senkrecht auf \(m\).
Mit Brennpunkt und Leitgeraden ist die Parabel nun eindeutig gegeben. Die Parabel ist die Menge aller Punkte \(P\), die vom Brennpunkt \(F\) und der Leitgeraden den selben Abstand haben (hellgrün).
Die Parameter der Parabel lassen sich aus der Zeichnung ablesen. Der Scheitel \(S\) (blau) liegt in der Mitte zwischen \(F\) und der Leitgeraden; also bei \((x_;\, y_s) = (3;\, 9)\) und der Faktor \(a\) berechnet sich aus dem sogenannten Halbparameter \(p\), das ist der Abstand vom Brennpunkt \(F\) zur Leitgeraden. hier ist \(p=-1\); negativ, da \(F\) unterhalb der Leitgeraden liegt. Und $$a = \frac 1{2p} = \frac{1}{2 \cdot (-1)} = - \frac 12 $$Mehr dazu findest Du hier.