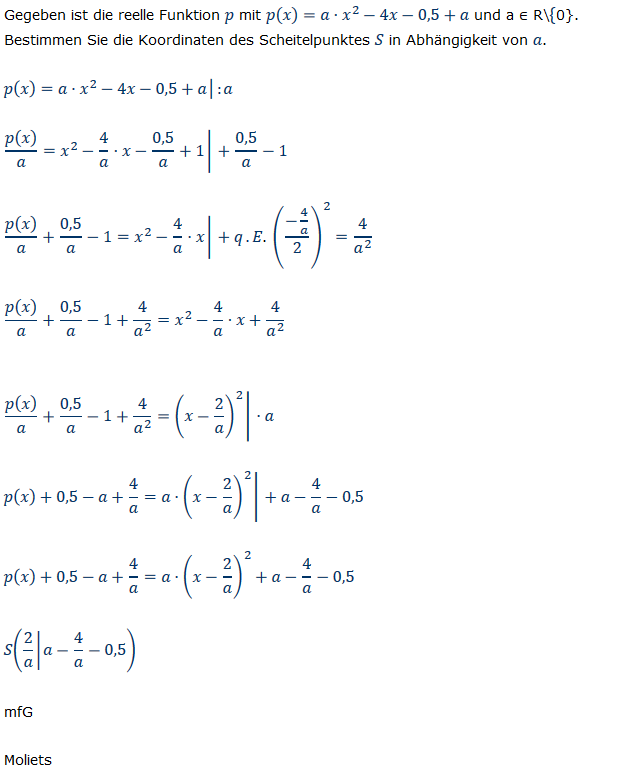
Text erkannt:
Gegeben ist die reelle Funktion \( p \) mit \( p(x)=a \cdot x^{2}-4 x-0,5+a \) und \( \mathrm{a} \in \mathrm{R} \backslash\{0\} \)
Bestimmen Sie die Koordinaten des Scheitelpunktes \( S \) in Abhängigkeit von \( a \).
\( p(x)=a \cdot x^{2}-4 x-0,5+a \mid: a \)
\( \frac{p(x)}{a}=x^{2}-\frac{4}{a} \cdot x-\frac{0,5}{a}+1 \mid+\frac{0,5}{a}-1 \)
\( \frac{p(x)}{a}+\frac{0,5}{a}-1=x^{2}-\frac{4}{a} \cdot x \mid+q \cdot E \cdot\left(\frac{-\frac{4}{a}}{2}\right)^{2}=\frac{4}{a^{2}} \)
\( \frac{p(x)}{a}+\frac{0,5}{a}-1+\frac{4}{a^{2}}=x^{2}-\frac{4}{a} \cdot x+\frac{4}{a^{2}} \)
\( \frac{p(x)}{a}+\frac{0,5}{a}-1+\frac{4}{a^{2}}=\left(x-\frac{2}{a}\right)^{2} \mid \cdot a \)
\( p(x)+0,5-a+\frac{4}{a}=a \cdot\left(x-\frac{2}{a}\right)^{2} \mid+a-\frac{4}{a}-0,5 \)
\( p(x)+0,5-a+\frac{4}{a}=a \cdot\left(x-\frac{2}{a}\right)^{2}+a-\frac{4}{a}-0,5 \)
\( S\left(\frac{2}{a} \mid a-\frac{4}{a}-0,5\right) \)
\( \operatorname{mfG} \)
Moliets