Der Term unter der Wurzel wird durch das Potenzieren mit 2 nie negativ, deswegen sind keine Bedingungen für \(x\) nötig. Demnach ist \(x\) eine beliebige, reelle Zahl. Für \(x>9\) wird der Ausdruck \(9-x\) negativ. Deshalb müssen beim Wurzelziehen die Betragsstriche gesetzt werden: $$\sqrt{(9-x)^2}=\lvert 9-x\rvert.$$ Wenn du die Betragsstriche weglassen würdest, dann könnte der Term \((9-x)^2\) nach dem Wurzelziehen negativ werden. Das ist aber unmöglich, weil \((9-x)^2\) immer positiv ist und demnach auch das Ergebnis des Wurzelziehens, nämlich \(9-x\). Also müssen Betragsstriche gesetzt werden!
Kleines Beispiel:
Für \(x=5\) ist \(\sqrt{(9-x)^2}=\sqrt{(9-5)^2}=\sqrt{4^2}=\sqrt{16}=4\).
Für \(x=14\): \(\sqrt{(9-14)^2}=\sqrt{(-5)^2}=\sqrt{25}=5\), der Ausdruck \(9-14=-5\) ist also negativ. Wir brauchen die Betragsstriche, sonst stimmt Ergebnis und der Ausgangsterm nicht überein.
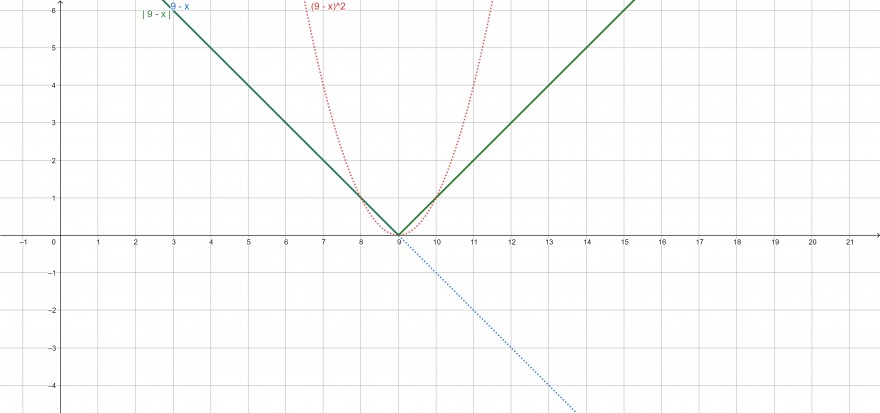
Hier noch einmal etwas anschaulicher: Die blaue Linie entspricht der Funktion \(g(x)=9-x\) während die grüne Linie der Funktion \(f(x)=\lvert 9-x \rvert\) entspricht. Im Vergleich dazu die quadratische Funktion \((9-x)^2\), die überall positiv oder 0 ist.