e-Funktion und ganzrationale Funktion

Question

Aufgabe:

Die Golden-Gate-Bridge war nach ihrer Erbauung im Jahr 1937 mehr als 25 Jahre lang die längste Brücke der Welt. Die beiden Hauptkabel sind an der Spitze der beiden Pfeile in 152m Höhe übee der Straße befestigt, der tiefste Punkt jedes der beiden Kabel befindet sich in ca. 20m Höhe über der Straße.

a) Beschreiben Sie die Lage des Kabels zwischen den beiden Pfeilern mit x, f(x) in m durch

(1) eine Parabel und

(2) durch eine sogenannte Kettenlinie der Form g(x)= a.(e^b.x + e^-b.x ) mit a, b > 0.

Stellen Sie die beiden Kurven in einem gemeinsamen Koordinatensystem graphisch dar. An welcher Stelle ist der Unterschied zwischen den beiden koordinatensystem graphisch dar.

b) In welchem Bereich steigt die Parabel schneller als die Kettenlinie? Wie groß ist jeweils die Steigung an der Pfeilerspitze?

Problem/Ansatz:

Ich verstehe die Aufgabe nicht. Es wäre sehr nett, wenn Sie es auflösen.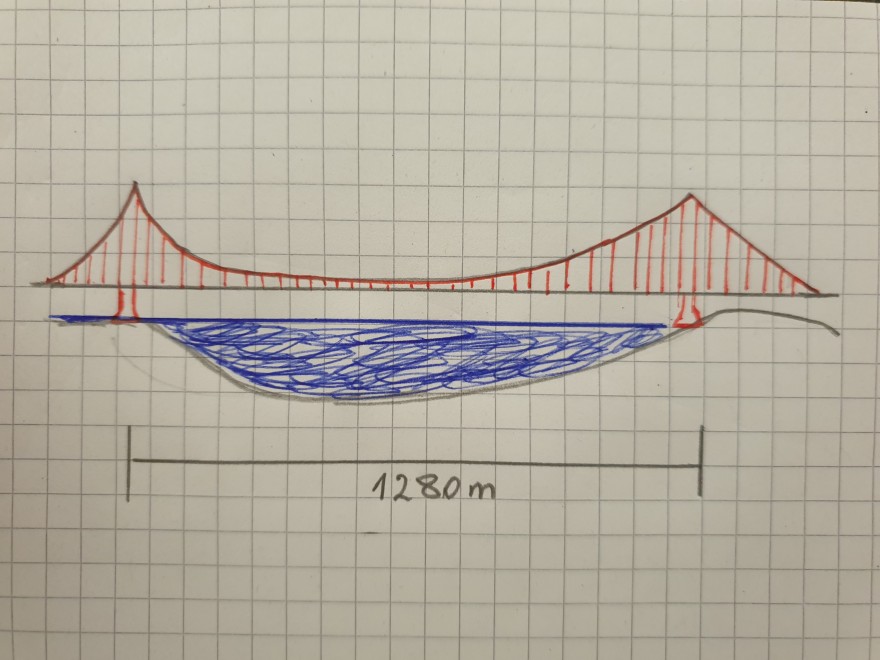

Text erkannt:

\begin{tabular}{l}
1. \\
\hline
\end{tabular}

Answer 1

Die Golden-Gate-Bridge war nach ihrer Erbauung im Jahr 1937 mehr als 25 Jahre lang die längste Brücke der Welt. Die beiden Hauptkabel sind an der Spitze der beiden Pfeile in 152m Höhe übee der Straße befestigt, der tiefste Punkt jedes der beiden Kabel befindet sich in ca. 20m Höhe über der Straße.

als Parabel
x = 0 = Mitte Brückelänge
h ( x ) = a * x^2 + c

f ( 0 | 20 )
f ( 640 | 152 )
h ( 0 ) = a * 0^2 + c = 20  => c = 20
h ( 640 ) = a * 640^2 + 20 = 152
a = 33 / 102400 = 0.000322265625

h ( x ) = 33 / 102400 * x + 20

Vielleicht ist die Frage schon erledigt.
Ansonsten frage nach.

Comments

Vielen vielen Dank

Jetzt hab ich verstanden.

---

Wie rechnet man die Kettenlinie?

---

Kettenlinie
g(x)= a * [ e^(b.*x) + e^(-b.*x ) ]
Mathematisch ist dies nur eine Funktion
mit 2 Parametern a und b
Es gilt wie bei der Parabel
g ( 0 | 20 )
g( 640 | 152 )
Einsetzen
g(0)= a * [ e^(b.*0) + e^(-b.*0 ) ] = 20
g(640)= a * [ e^(b*640) + e^(-b*640 ) ] = 152

a * [ e^(b *0) + e^(-b*0 ) ] = 20
a * [ e^(b*640) + e^(-b*640 ) ] = 152

a * [ e ^0 + e ^-0  ] = 20
a * ( 1 + 1 ) = 20
2*a = 20
a = 10

Einsetzen
10 * [ e^(b*640) + e^(-b*640 ) ] = 152
b = 0.004245216873

g ( x ) =
10 *
(
e^(+ 0.004245216873 * x +
e^ (- 0.004245216873 * x )
)
Falls die anderen Fragen noch nicht klar
sind dann frag weiter.

Answer 2

f(x) = 33/102400·x^2 + 20
g(x) = 10·(e^(0.004245216873·x) + e^(-0.004245216873·x))

Parabel: blau
Kettenlinie: rot

Comments

Ich gebe die Funktionen f(x) und g(x) in meiner Taschenrechner aber es zeigt gar nichts. Können Sie mir erklären, wie mann es in Taschenrechner geben kann?

---

Vielleicht ist nur eine falsche Skalierung eingestellt.

Da solltest du mal probieren und die Anleitung zu rate ziehen. Ich weiß weder welchen Taschenrechner du benutzt noch was du eingegeben hast.

---

Können Sie mir erklären, wie man 33/102400 und 0,004245216873 bekommt?

---

Schau mal ob du das von oswald verstehst.

Answer 3

a) Beschreiben Sie die Lage des Kabels zwischen den beiden Pfeilern mit x, f(x) in m

1. Stelle die allgemeine Funktionsgleichung auf.
2. Entnimm aus der Aufgabenstellung einen Punkt, der auf dem Graphen liegt. Setze ihn in die allgemeine Funktionsgleichung ein.
   
3. Wiederhole bis du so viele GLeichungen hast, wie Parameter in der allgemeinen Funktionsgleichung vorkommen.
4. Löse das Gleichungssystem.
   

durch (1) eine Parabel

Allgemeine Funktionsgleichung ist

        f(x) = ax² + bx + c.

Aus Teil (2) weiß ich aber, dass der Scheitelpunkt auf der y-Achse liegen soll. In diesem Fall reicht die allgemeine Funktionsgleichung

        f(x) = ax² + c.