Funktion 3. Grades stetigkeit

Question

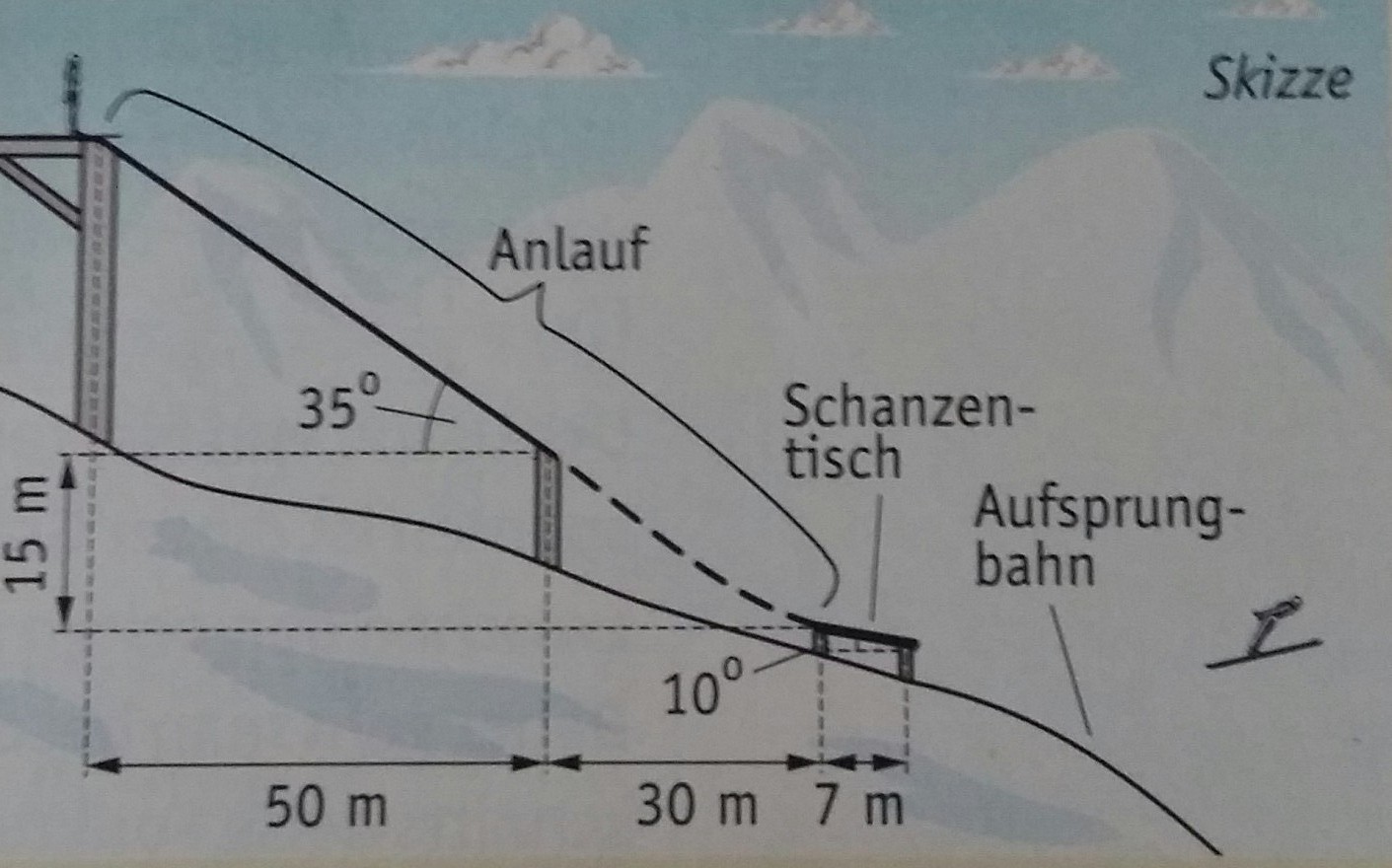
Die Abbildung, die ich gezeichnet habe, zeigt den Aufbau einer Skisprungschanze: Die Anlaufbahn besteht aus einem geradlinigen Teil mit Neigung (35°) und einem gekrümmten Stück (gestrichelt),dsnach erfolgt der Absprung vom geradlinigen Schanzentisch, der die Neigung (10°) hat.

Nach den Normen des FIS kann der gekrümmte Bereich (der Übergangsbogen) ein Kreisausschnitt oder eine kubische Parabel sein.


Problem/Ansatz: Ich muss eine ganzrationale Funktion dritten Grades zur Beschreibung des Übergangsbogens zwischen dem gradlinigen Teil des Anlaufs und dem Schanzentisch in der Skizze ermitteln.

Ich schicke auch meine Idee. Können Sie mich bitte weiter helfe?

…

Text erkannt:

\( f(x)=a x^{3}+b x^{2}+c x+d \)
\( 1-m \cdot x+b \)
P \( \log (1,5) \)
tusa \( 1,5=0,700003 \cdot 0,3 \cdot b \)
$$ y=a^{7}+0028 \cdot x+1,433 $$
2) \( y=m \cdot x+b \) \( P(0,5+65) \quad P(0,510) \)
\( \left(2 \tan 610^{\circ}\right)=0 / 176327 \)
$$ 0=0,176327+2,8+b $$

Answer 1

f(x) = a·x^3 + b·x^2 + c·x + d
f'(x) = 3·a·x^2 + 2·b·x + c

f(-30) = 15 → - 27000·a + 900·b - 30·c + d = 15
f'(-30) = TAN(-35°) → 2700·a - 60·b + c = TAN(-35°)
f(0) = 0 → d = 0
f'(0) = TAN(-10°) → c = TAN(-10°)

f(x) = 0.0001372·x^3 + 0.0149·x^2 - 0.1763·x