Quadrat in einem Dreieck: 1/t=1/b+1/c

Question

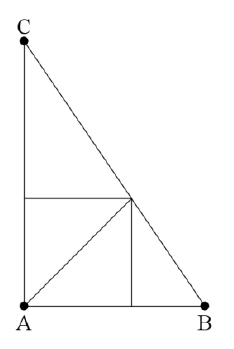
Aufgabe:

In einem rechtwinkligem Dreieck ABC wird ein Quadrat so wie in der Skizze eingepasst.

Zeige, dass dessen Seitenlänge t, so beschreiben werden kann: 1/t=1/b+1/c

Problem/Ansatz:

Hatte verschiedene Ansätze, welche aber nicht funktioniert hatten:

Man könnte zum Beispiel den Satz für ähnliche Dreiecke verwenden, wodurch wir zum Beispiel:

b/c= (b/t)/t

hätten.

Bräuchte bei dieser Herleitung etwas Hilfe.

Text erkannt:

\( \lambda \)

Answer 1

Betrachte die Fläche des Dreiecks A = b*c / 2

und zerlege sie in 3 Teile

t^2 + (c-t)*t / 2  +  ( b-t ) *t / 2

und setze sie gleich und löse nach 1/t auf.

Answer 2

Mit den Strahlensätzen erhalte ich \( \frac{c-t}{t} \)=\( \frac{c}{b} \). Umformen ergibt. \( \frac{c}{t} \)-1=\( \frac{c}{b} \) und nach Division durch c: \( \frac{1}{t} \) - \( \frac{1}{c} \)=\( \frac{1}{b} \). Jetzt noch \( \frac{1}{c} \) auf beiden Seiten addieren.

Answer 3

Die Gerade von B nach C lässt sich beschreiben durch

y = b - b/c·x

Nun gilt für den Punkt P als rechte obere Ecke des Quadrates, dass t = x = y ist. Also

t = b - b/c·t
t/b = 1 - 1/c·t
1/b = 1/t - 1/c
1/b + 1/c = 1/t

Answer 4

$$2A_{ABC}=2A_{ABF} +2A_{AFC}$$$$b*c=t*b+t*c$$$$\frac{1}{t} = \frac{b+c}{bc}$$$$\frac{1}{t} = \frac{c}{bc}+\frac{b}{bc}$$$$\frac{1}{t} = \frac{1}{b}+\frac{1}{b}$$